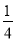��Ŀ����
���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�������н�������ȷ���ǣ�������
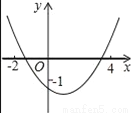
A. c����1 B. b��0 C. 2a+b��0 D. 9a+c��3b
D ������������������y��Ľ����ڵ㣨0����1�����·��õ�c����1���������߿��ڷ����a��0�����������ߵĶԳ�����y����Ҳ��a��b��ţ���b��0�����������ߵĶԳ��Եõ������߶Գ���Ϊֱ��x=������x=1����2a+b=0���ʿ��ܳ��������ڵ�x=��3ʱ��y��0������9a��3b+c��0����9a+c��3b�� �������� ����������y��Ľ����ڵ㣨0����1�����·��� ��c����1�� ...
��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ


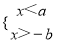 B.
B. 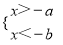 C.
C. 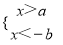 D.
D. 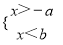
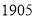 ���峯ѧ�õĿα����á�
���峯ѧ�õĿα����á�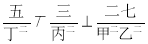 ������ʾ�൱�ڡ�
������ʾ�൱�ڡ�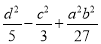 ������ô��
������ô��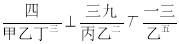 ����ʾ�൱��__________��
����ʾ�൱��__________��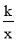 ��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��
��k��0��������OB���е�C��AE���е�D����֪�ȱߡ�OAB�ı߳�Ϊ4��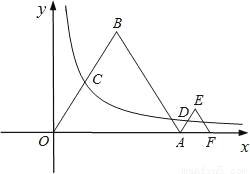
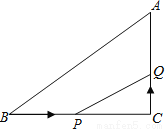
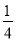 ��a��0 B. a��
��a��0 B. a��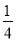 C. a��
C. a��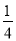 ��a��0 D. a��
��a��0 D. a��