题目内容
如下图,△ABC中,∠C=30°.将△ABC绕点A顺时针旋转60°得到△ADE,AE与BC交于F,则∠AFB= °.

90°.
【解析】
试题分析:根据旋转的性质可知∠CAF=60°;然后在△CAF中利用三角形内角和定理可以求得∠CFA=90°,即∠AFB=90°.
试题解析:∵△ADE是由△ABC绕点A顺时针旋转60°得到的,
∴∠CAF=60°;
又∵∠C=30°
∴在△AFC中,∠CFA=180°-∠C-∠CAF=90°,
∴∠AFB=90°.
考点:旋转的性质.

练习册系列答案
相关题目
 ABC中,∠C=90°,∠BAC=60°,AB=8.半径为
ABC中,∠C=90°,∠BAC=60°,AB=8.半径为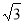 的⊙M与射线BA相切,切点为N,且AN=3.将Rt
的⊙M与射线BA相切,切点为N,且AN=3.将Rt 后得到Rt
后得到Rt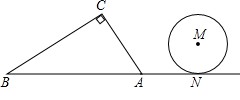
 的顶点在坐标轴上,则m= 。
的顶点在坐标轴上,则m= 。

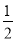 B.
B.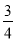 C.
C.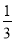 D.
D.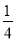
 的部分图象如图所示,由图可知,关于x的方程
的部分图象如图所示,由图可知,关于x的方程 的
的