Question

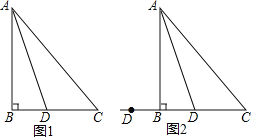
【题目】如图，在直角三角形中，，点，分别为，的中点，将沿翻折，得到，的延长线交于点．

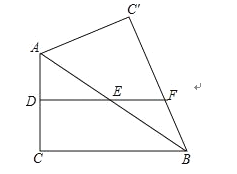
（1）判断的形状为 ；

（2）当时，求证四边形为正方形；

（3）若，连接，当时，直接写出的长．

Answer 1

【答案】（1）等腰三角形；（2）见解析；（3）

【解析】

（1）根据三角形中位线的性质得到DE∥BC，求得∠BEF=∠ABC，根据折叠的性质得到∠ABC=∠ABC′，求得∠BEF=∠EBF，于是得到结论；
（2）根据折叠的性质得到∠C′=∠C=90°，AC=AC′，根据平行线的判定定理得到DF∥AC′，推出四边形ACBC′是矩形，由于AC=AC′，于是得到四边形ACBC′是正方形；
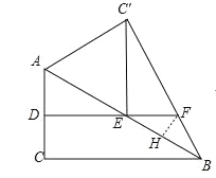
（3）根据直角三角形的性质得到C′E=BE=AE=AB=2，求得∠EC′B=∠C′BE，过F作FH⊥BE，根据等腰三角形的性质得到∠EFH=∠BFH，根据平角的定义得到∠C′FE=∠FEH=60°，于是得到∠ADE=∠FEH=30°，解直角三角形即可得到结论．

解：（1）∵点，分别为，的中点，

，

，

∵将沿翻折，得到，

，

，

是等腰三角形；

故答案为：等腰三角形；

（2）∵将沿翻折，得到，

，，

，

，

，

，

，

，

∴四边形是矩形，

，

∴四边形是正方形；

（3）为的中点，

，

，

过作，

，

，

，

，

，

，

，

，

，

，

，，

．