Question

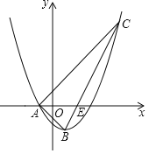
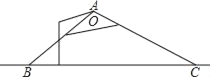
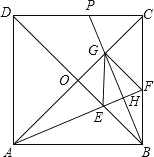
【题目】如图，正方形ABCD中，对角线AC、BD交于点O，∠BAC的平分线交BD于E，交BC于F，BH⊥AF于H，交AC于G，交CD于P，连接GE、GF，以下结论：①△OAE≌△OBG；②四边形BEGF是菱形；③BE＝CG；④﹣1；⑤S△PBC：S△AFC＝1：2，其中正确的有（　　）个．

A.2B.3C.4D.5

Answer 1

【答案】C

【解析】

根据AF是∠BAC的平分线，BH⊥AF，可证AF为BG的垂直平分线，然后再根据正方形内角及角平分线进行角度转换证明EG＝EB，FG＝FB，即可判定②选项；设OA＝OB＝OC＝a，菱形BEGF的边长为b，由四边形BEGF是菱形转换得到CF＝GF＝BF，由四边形ABCD是正方形和角度转换证明△OAE≌△OBG，即可判定①；则△GOE是等腰直角三角形，得到GE＝OG，整理得出a，b的关系式，再由△PGC∽△BGA，得到＝1+，从而判断得出④；得出∠EAB＝∠GBC从而证明△EAB≌△GBC，即可判定③；证明△FAB≌△PBC得到BF＝CP，即可求出，从而判断⑤.

解：∵AF是∠BAC的平分线，

∴∠GAH＝∠BAH，

∵BH⊥AF，

∴∠AHG＝∠AHB＝90°，

在△AHG和△AHB中

，

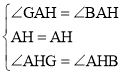∴△AHG≌△AHB（ASA），

∴GH＝BH，

∴AF是线段BG的垂直平分线，

∴EG＝EB，FG＝FB，

∵四边形ABCD是正方形，

∴∠BAF＝∠CAF＝×45°＝22.5°，∠ABE＝45°，∠ABF＝90°，

∴∠BEF＝∠BAF+∠ABE＝67.5°，∠BFE＝90°﹣∠BAF＝67.5°，

∴∠BEF＝∠BFE，

∴EB＝FB，

∴EG＝EB＝FB＝FG，

∴四边形BEGF是菱形；②正确；

设OA＝OB＝OC＝a，菱形BEGF的边长为b，

∵四边形BEGF是菱形，

∴GF∥OB，

∴∠CGF＝∠COB＝90°，

∴∠GFC＝∠GCF＝45°，

∴CG＝GF＝b，∠CGF＝90°，

∴CF＝GF＝BF，

∵四边形ABCD是正方形，

∴OA＝OB，∠AOE＝∠BOG＝90°，

∵BH⊥AF，

∴∠GAH+∠AGH＝90°＝∠OBG+∠AGH，

∴∠OAE＝∠OBG，

在△OAE和△OBG中

，

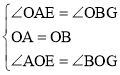∴△OAE≌△OBG（ASA），①正确；

∴OG＝OE＝a﹣b，

∴△GOE是等腰直角三角形，

∴GE＝OG，

∴b＝（a﹣b），

整理得a＝b，

∴AC＝2a＝（2+）b，AG＝AC﹣CG＝（1+）b，

∵四边形ABCD是正方形，

∴PC∥AB，

∴＝＝＝1+，

∵△OAE≌△OBG，

∴AE＝BG，

∴＝1+，

∴＝＝1﹣，④正确；

∵∠OAE＝∠OBG，∠CAB＝∠DBC＝45°，

∴∠EAB＝∠GBC，

在△EAB和△GBC中

，

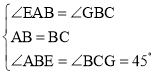∴△EAB≌△GBC（ASA），

∴BE＝CG，③正确；

在△FAB和△PBC中

，

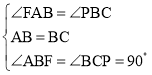∴△FAB≌△PBC（ASA），

∴BF＝CP，

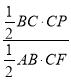∴＝＝＝＝，⑤错误；

综上所述，正确的有4个，

故选：C．