��Ŀ����
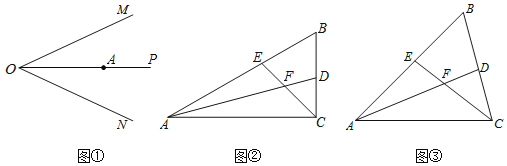
����Ŀ����1����ͼ����OP�ǡ�MON��ƽ���ߣ���AΪOP��һ�㣬������һ����BAC��B��C�ֱ���OM��ON�ϣ���ʹAOƽ�֡�BAC��������ͼ�ۼ�����
��2����ͼ�����ڡ�ABC�У���ACB��ֱ�ǣ���B��60�㣬��ABC��ƽ����AD��CE�ཻ�ڵ�F�������ж�FE��FD֮���������ϵ������ȣ�1���еķ�������
��3����ͼ�����ڡ�ABC�У������ACB��90�㣬����2���е������������䣬���ʣ�2�������õĽ����Ƿ���Ȼ����������������֤��������������˵�����ɣ�
���𰸡���1�������������2��FE��FD��֤�������������3��������֤�����������
��������
��1��������OM��ON�Ϸֱ��ȡOB��OC������AB��AC����AOƽ�֡�BAC��
��2������F��FG��AB��G����FH��BC��H����FK��AC��K�����ݽ�ƽ�����ϵĵ㵽�ǵ����ߵľ�����ȿɵ�FG��FH��FK�������ı��ε��ڽǺͶ��������GFH��120�㣬�ٸ��������ε��ڽǺͶ��������AFC��120�㣬���ݶԶ�����������EFD��120�㣬Ȼ�������EFG����DFH�������á��ǽDZߡ�֤����EFG�͡�DFHȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�FE��FD��
��3������F�ֱ���FG��AB�ڵ�G��FH��BC�ڵ�H������֤����GEF����HDF����֤����EGF�ա�DHF�ɵ�FE��FD��
�⣺��1����ͼ����ʾ����BAC��Ϊ����

��2����ͼ��������F��FG��AB��G����FH��BC��H����FK��AC��K��

��AD��CE�ֱ��ǡ�BAC����BCA��ƽ���ߣ�
��FG��FH��FK��
���ı���BGFH�У���GFH��360�㩁60�㩁90���2��120�㣬
��AD��CE�ֱ��ǡ�BAC����BCA��ƽ���ߣ���B��60�㣬
���FAC+��FCA��![]() ��180�㩁60�㣩��60�㣬
��180�㩁60�㣩��60�㣬
�ڡ�AFC�У���AFC��180�㩁����FAC+��FCA����180�㩁60�㣽120�㣬
���EFD����AFC��120�㣬
���EFD����GFH
���EFG����DFH��
�ڡ�EFG�͡�DFH�У�
 ��
��
���EFG�ա�DFH��ASA����
��FE��FD��
��3��������
���ɣ���ͼc������F�ֱ���FG��AB�ڵ�G��FH��BC�ڵ�H��

���FGE����FHD��90�㣬
�ߡ�B��60�㣬��AD��CE�ֱ��ǡ�BAC����BCA��ƽ���ߣ�
���FAC+��FCA��60�㣬F�ǡ�ABC�����ģ�
���GEF����BAC+��FCA��60��+��BAD��
��F�ǡ�ABC�����ģ���F�ڡ�ABC�Ľ�ƽ�����ϣ�
��FG��FH����ƽ�����ϵĵ㵽�ǵ�������ȣ���
�֡ߡ�HDF����B+��BAD��60��+��BAD����ǵ����ʣ���
���GEF����HDF��
�ڡ�EGF���DHF�У�
 ��
��
���EGF�ա�DHF��AAS����
��FE��FD��

 Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д�
Ӯ�ڿ�����ʦ��ʱ�ƻ�ϵ�д� �������Ͽ�ʱͬ��ѵ��ϵ�д�
�������Ͽ�ʱͬ��ѵ��ϵ�д�