题目内容
2. 如图,如果从半径为9cm的圆形纸片前去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )
如图,如果从半径为9cm的圆形纸片前去$\frac{1}{3}$圆周的一个扇形,将留下的扇形围成一个圆锥(接缝处不重叠),那么这个圆锥的高为( )| A. | 6cm | B. | 8cm | C. | 3$\sqrt{5}$cm | D. | 5$\sqrt{3}$cm |
分析 圆锥的底面圆半径为r,先利用圆的周长公式计算出剩下的扇形的弧长,然后把它作为圆锥的底面圆的周长进行计算即可求得底面圆的半径,然后利用勾股定理即可求得圆锥的高.
解答 解:∵从半径为9cm的圆形纸片剪去$\frac{1}{3}$圆周的一个扇形,
∴留下的扇形圆心角为:360°×$\frac{2}{3}$=240°,
∴留下的扇形的弧长=$\frac{240π×9}{180}$=12π,
根据底面圆的周长等于扇形弧长,
∴圆锥的底面半径r=$\frac{12π}{2π}$=6cm,
所以圆锥的高=$\sqrt{{9}^{2}-{6}^{2}}$=3$\sqrt{5}$cm.
故选C.
点评 此题主要考查了圆锥的性质,要知道(1)圆锥的高,底面半径,母线构成直角三角形,(2)此扇形的弧长等于圆锥底面周长,扇形的半径等于圆锥的母线长.解此类题目要根据所构成的直角三角形的勾股定理作为等量关系求解.

练习册系列答案
相关题目
12.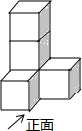 由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
 由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )
由五个完全相同的正方体组成如图的几何体,则下列说法正确的是( )| A. | 左视图与俯视图相同 | B. | 左视图与主视图相同 | ||
| C. | 主视图与俯视图相同 | D. | 三种视图都相同 |
13. 若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
 若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )
若一次函数y=kx+b的图象如图所示,则y<0时自变量x的取值范围是( )| A. | x>2 | B. | x<2 | C. | x>-1 | D. | x<-1 |
10.计算3x3•(-2x2)的结果是( )
| A. | -6x5 | B. | -6x6 | C. | -x5 | D. | x5 |
17.为节能减排,郑州市政府鼓励居民节约用电,为了解居民用电情况,在某小区随机抽查了20户家庭的月用电量,结果如表:
则关于这20户家庭的月用电量,下列说法正确的是( )
| 月用电量(度) | 4 | 5 | 6 | 8 | 9 |
| 户数 | 2 | 5 | 7 | 4 | 1 |
| A. | 中位数是5度 | B. | 众数是6度 | C. | 平均数是6度 | D. | 极差是4度 |
14.在某校初三年级古诗词比赛中,初三(1)班60名学生的成绩统计如下:
则该班学生成绩的中位数和众数分别是( )
| 分数 | 50 | 60 | 70 | 80 | 90 | 100 |
| 人数 | 1 | 2 | 8 | 23 | 22 | 4 |
| A. | 80,80 | B. | 70,80 | C. | 80,90 | D. | 90,80 |
11.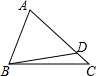 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
 如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )
如图所示,点D是△ABC的边AC上一点(不含端点),AD=BD,则下列结论正确的是( )| A. | AC>BC | B. | AC=BC | C. | ∠A>∠ABC | D. | ∠A=∠ABC |
12.下列各数中,最小的数是( )
| A. | 3 | B. | 0 | C. | -2 | D. | -3 |