题目内容
 如图:△AOB是直角边长为4的等腰三角形,C在OA上且OC=3,P是线段AB上的动点.当OP+CP最小时,(1)求出OP+CP的最小值.(2)求此时P点坐标.
如图:△AOB是直角边长为4的等腰三角形,C在OA上且OC=3,P是线段AB上的动点.当OP+CP最小时,(1)求出OP+CP的最小值.(2)求此时P点坐标.
分析:(1)先作C点关于AB的对称点C′,连接OC′、AC′,由两点之间线段最短可知OC′即为OP+CP的最小值,由对称的性质可知△AOC′是直角三角形,利用勾股定理即可求解;
(2)由OC′的长可求出C′点的坐标,根据△AOB是直角边长为4的等腰三角形可求出A、B两点的坐标,再用待定系数法分别求出过A、B及过O、C两点的一次函数解析式,求出其交点坐标即可.
(2)由OC′的长可求出C′点的坐标,根据△AOB是直角边长为4的等腰三角形可求出A、B两点的坐标,再用待定系数法分别求出过A、B及过O、C两点的一次函数解析式,求出其交点坐标即可.
解答: 解:(1)作C点关于AB的对称点C′,连接OC′、AC′,由两点之间线段最短可知OC′即为OP+CP的最小值,
解:(1)作C点关于AB的对称点C′,连接OC′、AC′,由两点之间线段最短可知OC′即为OP+CP的最小值,
∵C′是C关于AB的对称点,
∴AC=AC′=1,∠CAB=∠C′AB=45°,
∴∠CAC′=90°,
∵OA=4,AC′=1,
∴OC′=
=
=
;
(2)∵OC′=
,OA=4,AC′=1,
∴C′点的坐标为:(4,1),
∴设过O、C′两点的函数解析式为y=kx(k≠0),即k=
,
∴此一次函数的解析式为y=
x;
∵△AOB是直角边长为4的等腰三角形,
∴A(0,4)、B(4,0),
设过A、B两点的一次函数的解析式为y=kx+b(k≠0),
∴
,解得k=-1,b=4,
∴此一次函数的解析式为y=-x+4,
∴
,解得x=
,y=
,
∴P点坐标为(
,
).
故答案为:
,(
,
).
 解:(1)作C点关于AB的对称点C′,连接OC′、AC′,由两点之间线段最短可知OC′即为OP+CP的最小值,
解:(1)作C点关于AB的对称点C′,连接OC′、AC′,由两点之间线段最短可知OC′即为OP+CP的最小值,∵C′是C关于AB的对称点,
∴AC=AC′=1,∠CAB=∠C′AB=45°,
∴∠CAC′=90°,
∵OA=4,AC′=1,
∴OC′=
| OA2+AC′2 |
| 42+12 |
| 17 |
(2)∵OC′=
| 17 |
∴C′点的坐标为:(4,1),
∴设过O、C′两点的函数解析式为y=kx(k≠0),即k=
| 1 |
| 4 |
∴此一次函数的解析式为y=
| 1 |
| 4 |
∵△AOB是直角边长为4的等腰三角形,
∴A(0,4)、B(4,0),
设过A、B两点的一次函数的解析式为y=kx+b(k≠0),
∴
|
∴此一次函数的解析式为y=-x+4,
∴
|
| 16 |
| 5 |
| 4 |
| 5 |
∴P点坐标为(
| 16 |
| 5 |
| 4 |
| 5 |
故答案为:
| 17 |
| 16 |
| 5 |
| 4 |
| 5 |
点评:本题考查的是最短线路问题及用待定系数法求一次函数的解析式,根据题意作出图形,利用数形结合求解是解答此题的关键.

练习册系列答案
相关题目
 如图,∠AOB是直角,OD平∠BOC,OE平分∠AOC.
如图,∠AOB是直角,OD平∠BOC,OE平分∠AOC.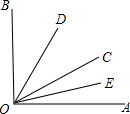
 25、如图,∠AOB是直角,∠COD也是直角,若∠AOC=α,则∠BOD等于( )
25、如图,∠AOB是直角,∠COD也是直角,若∠AOC=α,则∠BOD等于( )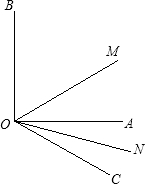 已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线.
已知:如图,∠AOB是直角,∠AOC=40°,ON是∠AOC的平分线,OM是∠BOC的平分线. 如图,∠AOB是直角,OB平分∠COD,∠COD=40°,则∠AOD=
如图,∠AOB是直角,OB平分∠COD,∠COD=40°,则∠AOD=