题目内容
现有一张矩形纸片ABCD(如图),其中AB=4cm,BC=6cm,点E是BC的中点.将纸片沿直线AE折叠,点B落在四边形AECD内,记为点B′,过E作EF垂直B′C,交B′C于F.
(1)求AE、EF的位置关系
(2)求线段B′C的长,并求△B′EC的面积

解:(1)由折线法及点E是BC的中点,
∴EB=EB′=EC,∠AEB=∠AEB′①
∴△B'EC是等腰三角形…………………………1分
 又∵EF⊥B′C∴EF为∠B'EC的角平分线,即∠B′EF=∠FEC②
又∵EF⊥B′C∴EF为∠B'EC的角平分线,即∠B′EF=∠FEC②
由①②得,∠AEF=90°,即AE⊥EF……………………2分
(2)由上题可知:∠AB′E=∠AEF=90°,
∠B′AE=∠B′EF(同角的余角相等),……………………1分
又∵△B'EC是等腰三角形,EF⊥B′C
∴ B′F=FC
∴△B′AE∽△FB′E ………………2分
又∵BE=3,AB=4,∠B=90°,∴AE=5
∴AE:EB′= EB′: B′F
∴B′F= ……………………………2分
……………………………2分
由题意可知四边形OEFB′是矩形,
∴EF=OB′= ∴S△B′EC=
∴S△B′EC= ×B′C•EF=
×B′C•EF= ×
× ×
× =
= …………2分
…………2分

练习册系列答案
相关题目
如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0),下列结论中,正确的一项是( )
|
| A.2a+b | <0 | B. | 3a+c<0 | C. | a+b+c>0 | D. | 4ac﹣b2<0 |
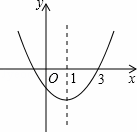
 (1)当△ABC为等腰直角三角形时,求
(1)当△ABC为等腰直角三角形时,求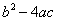 的值;
的值; 的解集为
的解集为 ,那么
,那么 的值等于____ ____。
的值等于____ ____。
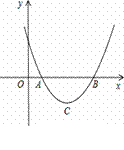
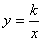 在第二象限内的图象如图所示,经过图象上两点A、E分别引
在第二象限内的图象如图所示,经过图象上两点A、E分别引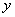 轴与
轴与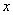 轴的垂线,交于点C,且与
轴的垂线,交于点C,且与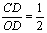 ,连接OA,OE,如果△AOC的面积是15,则△ADC与△BOE的面积和为
,连接OA,OE,如果△AOC的面积是15,则△ADC与△BOE的面积和为 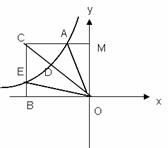
 B.
B. C.
C. D.
D. 
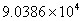 B.
B.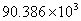 C.
C.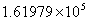 D.
D.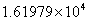
 的直径,弦CD⊥AB于点E,点P在
的直径,弦CD⊥AB于点E,点P在 ,求
,求