Question

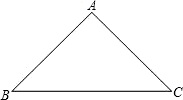
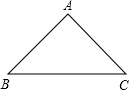
如图，△ABC是某小区的一块空地，现要加以绿化，其中点O是空地内安装喷泉的位置，它到三边的距离相等，即OD=OE=OF=m，现测得m=8.48米，三边长a=41米，b=34米，c=25米．利用因式分解求这块空地的面积．
（1）这快空地的面积用含a、b、c、m的代数式表示为

1

2

ma+

1

2

mb+

1

2

mc

；
（2）利用因式分解求这块空地的面积．

Answer 1

分析：（1）三角形ABC的面积等于三个三角形面积的和，利用三角形的面积公式进行计算即可；
（2）提取公因式因式分解后代入数值求解即可．

解答：解：（1）空地的面积为：S_△ABO+S_△BCO+S_△ACO=

1

2

ma+

1

2

mb+

1

2

mc
（2）原式=

1

2

m（a+b+c）
当m=8.48，a=41，b=34，c=25时，
原式=

1

2

×8.48×（41+34+25）=

1

2

×8.48×100=424平方米
答：这块空地的面积为424平方米．

点评：本题考查了因式分解的应用，题目中涉及到的因式分解至用到了提公因式法．