题目内容
(1)已知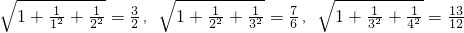 ,…试猜测
,…试猜测 的结果,并加以证明;
的结果,并加以证明; =
=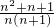 ,
,
(2)s=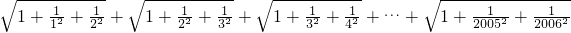 ,
,
求不超过S的最大整数[s].
解:(1)猜想: =
=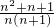 .
.
证明: =
=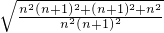 =
=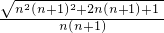 =
=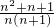 ;
;
(2)∵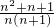 =1+
=1+ -
- ,
,
∴s=1+1- +1+
+1+ -
- +1+
+1+ -
- +…+1+
+…+1+ -
- =2005+1-
=2005+1- =2005
=2005 ,
,
∴[s]=2005.
分析:(1)观察几道算式可知,结果的分母为二次根式中两个分母的积,分子比分母大1,由此得出一般规律;
(2)将一般规律的结果变形,即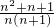 =1+
=1+ -
- ,再将n的值代入寻找抵消规律.
,再将n的值代入寻找抵消规律.
点评:本题考查了二次根式的化简求值.关键是根据算式发现一般规律,运用一般规律代值计算,寻找算式的抵消规律.
 =
=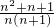 .
.证明:
 =
=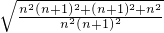 =
=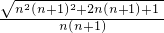 =
=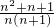 ;
;(2)∵
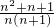 =1+
=1+ -
- ,
,∴s=1+1-
 +1+
+1+ -
- +1+
+1+ -
- +…+1+
+…+1+ -
- =2005+1-
=2005+1- =2005
=2005 ,
,∴[s]=2005.
分析:(1)观察几道算式可知,结果的分母为二次根式中两个分母的积,分子比分母大1,由此得出一般规律;
(2)将一般规律的结果变形,即
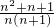 =1+
=1+ -
- ,再将n的值代入寻找抵消规律.
,再将n的值代入寻找抵消规律.点评:本题考查了二次根式的化简求值.关键是根据算式发现一般规律,运用一般规律代值计算,寻找算式的抵消规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
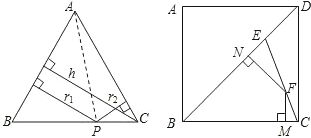
 已知,如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E;试猜测线段DE、AD、BE之间的数量关系,并说明理由.
已知,如图,在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E;试猜测线段DE、AD、BE之间的数量关系,并说明理由. 已知二次函数
已知二次函数