Question

在进行二次根式简化时，我们有时会碰上如，，一样的式子，其实我们还可将其进一步简化：

=；（一）

==；（二）

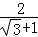===；（三）

以上这种化简的步骤叫做分母有理化

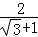还可以用以下方法化简：

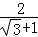===；（四）

（1）化简=__________=__________

（2）请用不同的方法化简．

①参照（三）式得=__________

②步骤（四）式得=__________

（3）化简：

+++…+．

Answer 1

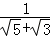【考点】分母有理化．

【专题】阅读型．

【分析】（1）根据题中所给出的例子把分母化为完全平方式的形式即可；

（2）①根据步骤（三）把分母乘以﹣即可；

②根据步骤（四）把分子化为（﹣）（+）的形式即可；

（3）把各式的分母有理化，找出规律即可得出结论．

【解答】解：（1）==，==．

故答案为：，；

（2）①原式==﹣．

故答案为：﹣；

②原式===﹣．

故答案为：﹣；

（3）原式=+++…+

=

=．

【点评】本题考查的是分母有理化，根据题意得出分母有理化的规律是解答此题的关键．