题目内容
 如图,等腰直角三角形OBA的直角顶点B在双曲线y﹦
如图,等腰直角三角形OBA的直角顶点B在双曲线y﹦| 6 |
| x |
(2
,0)
| 6 |
(2
,0)
.| 6 |
分析:首先过B作BE⊥AO,根据等腰直角三角形的性质可得∠BOA-45°,AO=2OE,再设B(m,m)进而得到m2=6,解可得m的值,进而得到A点坐标.
解答: 解:过B作BE⊥AO,
解:过B作BE⊥AO,
∵△AOB是等腰直角三角形,
∴∠BOA-45°,AO=2OE,
∵BE⊥AO,
∴∠OBE=45°,
∴OE=OB,
∴设B(m,m)
∵B点在双曲线y﹦
上,
∴m2=6,
m=±
,
∵B点在第一象限,
∴B(
,
),
∴AO=2OE=2
,
故答案为:(2
,0)
 解:过B作BE⊥AO,
解:过B作BE⊥AO,∵△AOB是等腰直角三角形,
∴∠BOA-45°,AO=2OE,
∵BE⊥AO,
∴∠OBE=45°,
∴OE=OB,
∴设B(m,m)
∵B点在双曲线y﹦
| 6 |
| x |
∴m2=6,
m=±
| 6 |
∵B点在第一象限,
∴B(
| 6 |
| 6 |
∴AO=2OE=2
| 6 |
故答案为:(2
| 6 |
点评:此题主要考查了反比例函数图象上点的坐标特点,以及等腰三角形的性质,关键是掌握反比例函数解析式图象上的点(x,y)的横纵坐标的积是定值k,即xy=k;

练习册系列答案
相关题目
 如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是
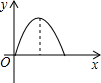
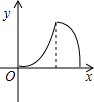
如图,等腰直角三角形ABC绕C点按顺时针旋转到△A1B1C1的位置(A、C、B1在同一直线上),∠B=90°,如果AB=1,那么AC运动到A1C1所经过的图形的面积是 如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )
如图,等腰直角三角形ABC的腰长与正方形DEFG的边长相符,且边AC与DE在同一直线l上,△ABC从如图所示的起始位置(A、E重合),沿直线l水平向右平移,直至C、D重合为止.设△ABC与正方形DEFG重叠部分的面积为y,平移的距离为x,则y与x之间的函数关系大致是( )

 如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M.
如图,等腰直角三角形ABC中,∠BAC=90°,D、E分别为AB、AC边上的点,AD=AE,AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M. 如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G.
如图,等腰直角三角形△ABC中,∠ACB=90°,点D是BC的中点,CE⊥AD于点F交AB于点E,CH是AB上的高交AD于点G. 如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.
如图,等腰直角三角形AEF的顶点E在等腰直角三角形ABC的边BC上.AB的延长线交EF于D点,其中∠AEF=∠ABC=90°.