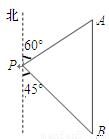题目内容
某学生参加社会实践活动,在景点P处测得景点B位于南偏东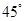 方向,然后沿北偏东
方向,然后沿北偏东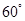 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.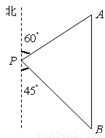
【答案】
(50+ )米
)米
【解析】
试题分析:过P作PD⊥AB,垂足为D,则∠A=60°,∠APD=30°,且PA=100米,即可求得AD的长,根据等角对等边可得DB=DP,根据勾股定理求得DP的长即可求得结果.
过P作PD⊥AB,垂足为D

∴∠A=60°,∠APD=30°,且PA=100米,
∴AD=50米
又∵∠B=∠DPB=45°
∴DB=DP
∵
∴AB=50+ 米
米
∴景点A与景点B之间的距离为(50+ )米.
)米.
考点:解直角三角形的应用
点评:解答本题的关键是读懂题意,正确作出辅助线,同时熟练应用三角函数的定义列方程求解.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
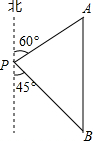 某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.
某学生参加社会实践活动,在景点P处测得景点B位于南偏东45°方向,然后沿北偏东60°方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离.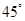 方向,然后沿北偏东
方向,然后沿北偏东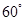 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之的距离.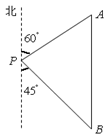
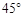 方向,然后沿北偏东
方向,然后沿北偏东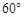 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
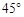 方向,然后沿北偏东
方向,然后沿北偏东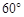 方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。
方向走100米到达景点A,此时测得景点B正好位于景点A的正南方向,求景点A与景点B之间的距离。