Question

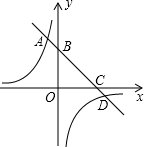如图，已知函数y=-x+1的图象与x轴，y轴分别交于C、B两点，与双曲线y=

k

x

（k≠0）交于A、D两点，若BC=2AB，则k的值为

 

．

Answer 1

分析：过A作AE⊥x轴于E点，易得到B点坐标为（0，1），C点坐标为（1，0）；由AE∥OB，根据三角形相似的判定定理得到△COB∽△CEA，再根据相似的性质得OB：AE=OC：EC=CB：CA，然后利用BC=2AB和OB=OC=1，可分别求出AE与OE，则可得到A点坐标，然后把A点坐标代入反比例的解析式即可求出k的值．

解答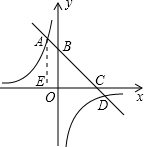：解：过A作AE⊥x轴于E点，如图，
对于y=-x+1，令x=0，则y=1；y=0，则x=1，
∴B点坐标为（0，1），C点坐标为（1，0）；
∵AE∥OB，
∴△COB∽△CEA，
∴OB：AE=OC：EC=CB：CA，
而BC=2AB，
∴OB：AE=OC：EC=2：3，
而OB=OC=1，
∴AE=EC=

3

2

，
∴OE=

3

2

-1=

1

2

，
∴A点坐标为（-

1

2

，

3

2

），
把A（-

1

2

，

3

2

）代入双曲线y=

k

x

（k≠0），
∴k=-

1

2

×

3

2

=-

3

4

．
故答案为-

3

4

．

点评：本题考查了点在反比例函数图象上，则点的横纵坐标满足其解析式．也考查了直线与坐标轴交点的求法以及三角形相似的判定与性质．