题目内容
 如图,一次函数y1=kx+2的图象与y轴交于点C,与反比例函数
如图,一次函数y1=kx+2的图象与y轴交于点C,与反比例函数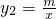 的图象交于A、B两点,点B的横坐标为-2,S△AOC=1,tan∠AOC=
的图象交于A、B两点,点B的横坐标为-2,S△AOC=1,tan∠AOC= .
.
(1)求一次函数与反比例函数的解析式;
(2)根据图象直接写出y1>y2时自变量x的取值范围.
 解:(1)过A作AH⊥y轴于H,
解:(1)过A作AH⊥y轴于H,∵在y1=kx+2中,令x=0得y=2,
∴C(0,2),
∴S△AOC=
 ×2×AH=1,
×2×AH=1,∴AH=1,
在Rt△AOH中,tan∠AOC=
 =
= ,
,∴OH=4,
∴A(1,4),
把A的坐标代入y1=kx+2得k=2,
∴一次函数的解析式是y1=2x+2;
把A的坐标代入y2=
 得:m=4,
得:m=4,∴反比例函数的解析式是y2=
 ;
;(2)∵A(1,4),B点的横坐标是-2,
∴y1>y2时自变量x的取值范围是-2<x<0或x>1.
分析:(1)过A作AH⊥y轴于H,
在y1=kx+2中令x=0得出y=2,求出C的坐标,根据三角形的面积公式求出AH,根据解直角三角形求出OH,得出A的坐标,分别把A的坐标代入一次函数和反比例函数的解析式即可求出答案;
(2)根据A、B点的横坐标结合图象即可得出答案.
点评:本题考查了用待定系数法求出反比例函数和一次函数的解析式,一次函数与反比例函数的交点问题等知识点的应用,用了数形结合思想.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
 如图,一次函数y1=kx+b的图象与反比例函数y2=
如图,一次函数y1=kx+b的图象与反比例函数y2=| m |
| x |
| A、-2<x<1 |
| B、0<x<1 |
| C、x<-2和0<x<1 |
| D、-2<x<1和x>1 |
 已知:如图,一次函数y1=kx+b(k≠0)的图象与反比例函数
已知:如图,一次函数y1=kx+b(k≠0)的图象与反比例函数 如图,一次函数y1=kx+b的图象与反比例函数
如图,一次函数y1=kx+b的图象与反比例函数 如图,一次函数y1=kx+1(k≠0)与反比例函数
如图,一次函数y1=kx+1(k≠0)与反比例函数 如图,一次函数y1=kx+b与反比例函数y2=-
如图,一次函数y1=kx+b与反比例函数y2=-