Question

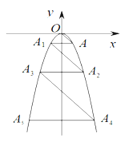
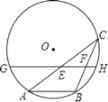
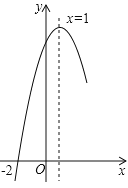
【题目】如图，已知二次函数的图象过点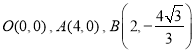，是中点.

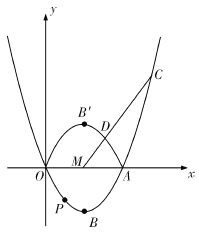
（1）求此二次函数的解析式.

（2）已知，点在抛物线上，点在轴上，当四点构成以为边的平行四边形，求此时点的坐标.

（3）将抛物线在轴下方的部分沿轴向上翻折，得曲线（为关于轴的对称点），在原抛物线轴的上方部分取一点，连接，与翻折后的曲线交于点. 若的面积是面积的3倍，这样的点是否存在？若存在，求出点的坐标，若不存在，请说明理由.

Answer 1

【答案】（1）二次函数解析式为：；（2）；（3）存在满足条件的点，点的坐标为.

【解析】

(1)利用待定系数法,代入A,B两点坐标，解一个含有a，b的二元一次方程组即可求得：

(2)存在这样的点有四个，运用平行四边形相关性质通过平移进行分类求解：

(3)为存在性问题通过的面积是面积的3倍这一关键信息进行分析求得.

（1）∵抛物线过原点，∴设其解析式为：

∵抛物线经过点，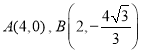

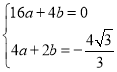∴，解得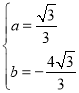

∴二次函数解析式为：

（2）点在抛物线上，Q的坐标为,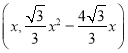

①当H,Q在直线PA下方时：

，，将P向右平移3个单位，向上平移个单位得到A，同样有点Q向右平移3个单位，向上平移个单位得到H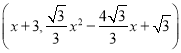,此时点在轴上，得到，求得x=3或1，此时H为（4,0）或（6,0）.

②当H,Q在直线PA上方时：同理可得H的坐标为.

综上H的坐标为 .

（3）依题意，翻折之后的抛物线解析式为：.

假设存在这样的点，

∵的面积是的面积的3倍，

∴，∴.

如图所示，分别过点作轴的垂线，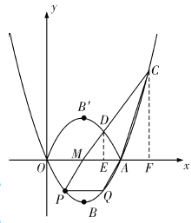

垂足分别为点、点，则有.

∴，∴.

设，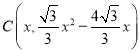

则，

∴.

∵，∴，

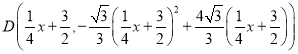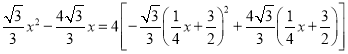整理得：，

解得：，

∴存在满足条件的点，点的坐标为.