题目内容

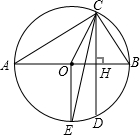
已知半径为R的圆中一条弧所对的圆周角为60°，那么它所对的弦长为（　　）
A．
2
R		B．2
2
R		C．
3
R		D．2
3
R
作直径AD，连接BD，
由圆周角定理得：∠C=∠D=60°，
∵AB是⊙O直径，
∴∠ABD=90°，
∴sin∠D=
AB
AD
，
∴AB=AD•sin60°=2R×
3
2
=
3
R．
故选C．
练习册系列答案
相关题目
△ABC内接于⊙O，且AB=AC，⊙O的半径等于6cm，O点到BC的距离OE等于3cm，则AC的长为______．
某小区一处圆柱形输水管道的圆形截面如图所示．若这个输水管道有水部分的水面宽AB=16cm，水面最深地方的高度CD为4cm．则这个圆形截面的半径是（　　）
A．20B．18C．12D．10
如图，已知直径MN⊥弦AB，垂足为C，下列结论：①AC=BC；②
AN
=
BN
；
AM
=
BM
；④AM=BM．其中正确的个数为（　　）
A．1B．2C．3D．4
如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，若AE=2，CD=8，则⊙O的半径为（　　）
A．4B．5C．8D．10
工人师傅设计了一个如图所示的工件槽，工件槽的两个底角均为90°，尺寸如图（单位cm）将形状规则的铁球放入槽内，若同时具有如图所示的A，B，E三个接触点，则该球半径的大小是（　　）
A．10cmB．18cmC．20cmD．22cm
如图，AB为⊙O直径，C为圆上任一点，作弦CD⊥AB，垂足为H．连接OC．
（1）说明∠ACO=∠BCD成立的理由；
（2）作∠OCD的平分线CE交⊙O于E，连接OE（点D、E可以重合），求出点E在弧ADB的具体位置，并说明理由；
（3）在（2）的条件下，连接AE，判断圆上是否存在点C，使△ACE为等腰三角形？若存在，请你写出∠CAE的度数．（不用写出推理过程）
如图，圆柱形水管内积水的水面宽度CD=8cm，F为
CD
的中点，圆柱形水管的半径为5cm，则此时水深GF的长度为______cm．
如图，P是⊙O内一定点，请你在⊙O内作出过P点的最长弦和最短弦，标上字母，并指出最长弦是______，最短弦是______．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网