��Ŀ����
��һ�����������ţ�����ˮλʱ������ˮ�����Ϊ20m��������ˮ��4m��
��1����ͼ��ʾ��ֱ������ϵ�У�����������ߵĹ�ϵʽ��
��2��������ˮλ�Ļ����ϣ���ˮλ����h��m��ʱ������ˮ��Ŀ���Ϊd��m���������d��ʾΪh�ĺ�����ϵʽ��
��3��������ˮλʱ�����µ�ˮ��Ϊ2m��Ϊ��֤������ֻ��˳��ͨ��������ˮ��Ŀ��Ȳ���С��18m����ˮ���������ʱ�ͻ�Ӱ�������ֻ������˳�����У�
��1����ͼ��ʾ��ֱ������ϵ�У�����������ߵĹ�ϵʽ��
��2��������ˮλ�Ļ����ϣ���ˮλ����h��m��ʱ������ˮ��Ŀ���Ϊd��m���������d��ʾΪh�ĺ�����ϵʽ��
��3��������ˮλʱ�����µ�ˮ��Ϊ2m��Ϊ��֤������ֻ��˳��ͨ��������ˮ��Ŀ��Ȳ���С��18m����ˮ���������ʱ�ͻ�Ӱ�������ֻ������˳�����У�

�⣺��1������κ�������ʽΪy=ax2��
����㣨10��-4���é�4=100a�����a=�� ��
��
��˶��κ�������ʽΪy=�� x2��
x2��
��2���ѵ㣨 ��4-h�����뺯������ʽy=-
��4-h�����뺯������ʽy=- x2����h=4-
x2����h=4- d2��
d2��
��3����x=9���뺯������ʽy=�� x2�У�
x2�У�
��y=�� ��92=��
��92=�� ���ף���
���ף���
��4+2�� =
= ��
��
�𣺵�ˮ��� ��ʱ������������ˮλ
��ʱ������������ˮλ ���ͻ�Ӱ�������ֻ������˳�����У�
���ͻ�Ӱ�������ֻ������˳�����У�
����㣨10��-4���é�4=100a�����a=��
 ��
����˶��κ�������ʽΪy=��
 x2��
x2����2���ѵ㣨
 ��4-h�����뺯������ʽy=-
��4-h�����뺯������ʽy=- x2����h=4-
x2����h=4- d2��
d2����3����x=9���뺯������ʽy=��
 x2�У�
x2����y=��
 ��92=��
��92=�� ���ף���
���ף�����4+2��
 =
= ��
���𣺵�ˮ���
 ��ʱ������������ˮλ
��ʱ������������ˮλ ���ͻ�Ӱ�������ֻ������˳�����У�
���ͻ�Ӱ�������ֻ������˳�����У�
��ϰ��ϵ�д�
�����Ŀ

 �ϵIJ��ֵĺ�����Ǿ���CDEF����ͼ����ƽ��ֱ������ϵ��
�ϵIJ��ֵĺ�����Ǿ���CDEF����ͼ����ƽ��ֱ������ϵ��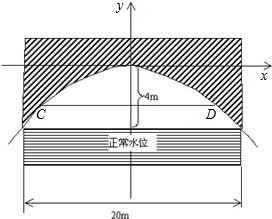 ��һ�����������ţ�����ˮλʱ������ˮ�����Ϊ20m��������ˮ��4m��
��һ�����������ţ�����ˮλʱ������ˮ�����Ϊ20m��������ˮ��4m��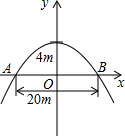 ��һ�����������ţ���ͼ��������ˮλʱ���º����20m��������4m��
��һ�����������ţ���ͼ��������ˮλʱ���º����20m��������4m��