题目内容
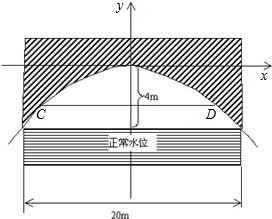 有一座抛物线型拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.
有一座抛物线型拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.(1)如图所示的直角坐标系中,求出该抛物线的关系式.
(2)在正常水位的基础上,当水位上升h(m)时,桥下水面的宽度为d(m),求出将d表示为h的函数关系式.
(3)设正常水位时,桥下的水深为2m,为保证过往船只的顺利通过,桥下水面的宽度不得小于18m,求水深超过多少米时就会影响过往船只在桥下顺利航行?
分析:(1)设出二次函数顶点式解析式,代入一个点的坐标即可解答;
(2)把点(
,-4+h)代入(1)中的函数解析式就可以解决;
(3)把点(9,0)代入(1)中的函数解析式就可以解决.
(2)把点(
| d |
| 2 |
(3)把点(9,0)代入(1)中的函数解析式就可以解决.
解答:解:(1)设二次函数解析式为y=ax2,
代入点(10,-4)得-4=100a,
解得a=-
,
因此二次函数解析式为y=-
x2;
(2)把点(
,-4+h)代入函数解析式y=-
x2,
得h=4-
d2;
(3)当桥下水面的宽度等于18m时,抛物线上第四象限点的横坐标为9,
把x=9代入函数解析式y=-
x2中,
∴y=-
×92=-
(米),
∴4+2-
=
.
答:当水深超过
米时,超过了正常水位
,就会影响过往船只在桥下顺利航行.
代入点(10,-4)得-4=100a,
解得a=-
| 1 |
| 25 |
因此二次函数解析式为y=-
| 1 |
| 25 |
(2)把点(
| d |
| 2 |
| 1 |
| 25 |
得h=4-
| 1 |
| 100 |
(3)当桥下水面的宽度等于18m时,抛物线上第四象限点的横坐标为9,
把x=9代入函数解析式y=-
| 1 |
| 25 |
∴y=-
| 1 |
| 25 |
| 81 |
| 25 |
∴4+2-
| 81 |
| 25 |
| 69 |
| 25 |
答:当水深超过
| 69 |
| 25 |
| 19 |
| 25 |
点评:此题考查待定系数法求函数解析式以及利用图象上的点解决实际问题.

练习册系列答案
相关题目

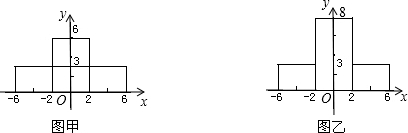
 上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.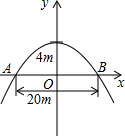 有一座抛物线型拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m.
有一座抛物线型拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m.