题目内容
12.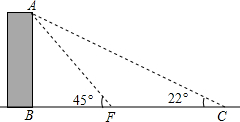 如图,某校有教学楼AB,当光线与地面的夹角是22°时,教学楼的影子为BC,当光线与地面的夹角是45°时,教学楼的影子为BF,学校要在A、C之间挂一些彩旗,现测得FC为13m(B、F、C在一条直线上),请你求出A、C之间的距离(结果保留整数)(参考数据:sin22°≈$\frac{3}{8}$,cos22°$≈\frac{15}{16}$,tan22°$≈\frac{2}{5}$)
如图,某校有教学楼AB,当光线与地面的夹角是22°时,教学楼的影子为BC,当光线与地面的夹角是45°时,教学楼的影子为BF,学校要在A、C之间挂一些彩旗,现测得FC为13m(B、F、C在一条直线上),请你求出A、C之间的距离(结果保留整数)(参考数据:sin22°≈$\frac{3}{8}$,cos22°$≈\frac{15}{16}$,tan22°$≈\frac{2}{5}$)
分析 在Rt△ABF中,设AB=BF=xm,在Rt△ABC中,得$\frac{\frac{26}{3}}{AC}$=sin22°,据此即可求出AC的长.
解答 解:设AB=BF=xm,
在Rt△ABC中,$\frac{x}{x+13}$=tan22°,
即$\frac{x}{x+13}$=$\frac{2}{5}$,
解得2x+26=5x,
x=$\frac{26}{3}$,
在Rt△ABC中,$\frac{\frac{26}{3}}{AC}$=sin22°,
即$\frac{\frac{26}{3}}{AC}$=$\frac{3}{8}$,
解得AC=$\frac{208}{9}$≈23.
答:A、C之间的距离为23米.
点评 本题考查了解直角三角形的应用,仰角俯角问题,要求学生能借助仰角构造直角三角形并解直角三角形.

练习册系列答案
相关题目
2.$\frac{2}{3}$的倒数是( )
| A. | $-\frac{2}{3}$ | B. | $\frac{2}{3}$ | C. | $-\frac{3}{2}$ | D. | $\frac{3}{2}$ |
20.同学们都知道,蜜蜂建造的蜂巢既坚固又省料,那你知道蜂巢的厚度吗?事实上,蜂巢厚度约为0.000073m,此数用科学记数法表示为( )
| A. | 7.3×10-4m | B. | 7.3×10-5m | C. | 7.3×105m | D. | 73×10-5m |
4.正五边形的每个外角等于( )
| A. | 36° | B. | 60° | C. | 72° | D. | 108° |
1. 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
 如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )
如图,数轴上两点A,B表示的数互为相反数,则点B表示的数为( )| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
 如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,
如图,已知直线y=$\frac{1}{2}$x与双曲线y=$\frac{k}{x}$(k>0)交于两点,且点A的横坐标为2,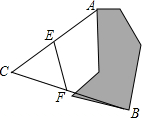 如图,现需测量池塘边上A、B两点间的距离,小强在池塘外选取一个点C,连接AC与BC并找到它们中点E、F,测得EF长为45米,则池塘的宽AB为90米.
如图,现需测量池塘边上A、B两点间的距离,小强在池塘外选取一个点C,连接AC与BC并找到它们中点E、F,测得EF长为45米,则池塘的宽AB为90米.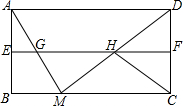 如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.
如图,在矩形ABCD中,AB=a,AD=b,E,F分别是AB,CD的中点,M是BC上一动点,AM,DM分别交EF于点G,H,连接CH.