题目内容
(1998•浙江)如图,正方形ABCD中,E、F分别是AB和AD上的点,已知CE⊥BF,垂足为M,求证:(1)∠EBM=∠ECB;(2)BE=AF.

【答案】分析:在Rt△BAF和Rt△EBC中,两直角相等,AB=BC,我们只要证明出另外有一组对应角相等就能够知道这两个三角形全等,从而得出结论.
解答:证明:∵CE⊥BF,垂足为M,
∴∠MBC+∠MCB=∠BEC+∠MCB,
∴∠MBC=∠BEC
又∵AD∥BC,
∴∠MBC=∠AFB
∴∠AFB=∠BEC,
又∵∠BAF=∠EBC,AB=BC,
∴Rt△BAF≌Rt△EBC,
∴(1)∠EBM=∠ECB;(2)BE=AF.
点评:这里主要考查了三角形全等判定定理中的AAS定理.
解答:证明:∵CE⊥BF,垂足为M,
∴∠MBC+∠MCB=∠BEC+∠MCB,
∴∠MBC=∠BEC
又∵AD∥BC,
∴∠MBC=∠AFB
∴∠AFB=∠BEC,
又∵∠BAF=∠EBC,AB=BC,
∴Rt△BAF≌Rt△EBC,
∴(1)∠EBM=∠ECB;(2)BE=AF.
点评:这里主要考查了三角形全等判定定理中的AAS定理.

练习册系列答案
相关题目

 (1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .
(1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .
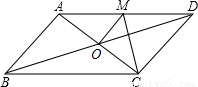 (1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .
(1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .