题目内容
 (1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .
(1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .
【答案】分析:根据题意,OM垂直平分AC,所以MC=MA,因此△CDM的周长=AD+CD,可得平行四边形ABCD的周长.
解答:解:∵ABCD是平行四边形,
∴OA=OC,
∵OM⊥AC,
∴AM=MC.
∴△CDM的周长=AD+CD=a,
∴平行四边形ABCD的周长是2a.
故答案为2a.
点评:此题考查了平行四边形的性质及周长的计算,根据线段垂直平分线的性质,证得AM=MC是解题的关键.
解答:解:∵ABCD是平行四边形,
∴OA=OC,
∵OM⊥AC,
∴AM=MC.
∴△CDM的周长=AD+CD=a,
∴平行四边形ABCD的周长是2a.
故答案为2a.
点评:此题考查了平行四边形的性质及周长的计算,根据线段垂直平分线的性质,证得AM=MC是解题的关键.

练习册系列答案
相关题目



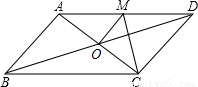 (1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .
(1998•浙江)如图,平行四边形ABCD的对角线相交于点O,且AD≠CD,过点O作OM⊥AC,交AD于点M.如果△CDM的周长为a,那么平行四边形ABCD的周长是 .