题目内容
已知二次函数 .
.
(1)求二次函数与 轴的交点坐标;
轴的交点坐标;
(2)求二次函数的对称轴和顶点坐标;
(3)写出y随x增大而减小时自变量x的取值范围.
(1)(1,0)和(3,0);(2)直线x=2,(2,-1);(3)x<2.
【解析】
试题分析:(1)求二次函数与x轴的交点坐标,即当y=0时,得到关于x的一元二次方程,计算x的值,即可得到交点的横坐标,纵坐标为0;
(2)通过配方得到顶点式的二次函数解析式,直接写出二次函数的对称轴和顶点坐标;
(3)借助对称轴得到y随x的增大而减小时的自变量x的取值范围.
试题解析:【解析】
(1)令  ,则
,则 ,解得
,解得 或
或 ,
,
∴二次函数与 轴的交点坐标为(1,0)和(3,0);
轴的交点坐标为(1,0)和(3,0);
(2) ,
,
 ,
,
=
∴抛物线的对称轴是直线 ,顶点坐标是(2,-1);
,顶点坐标是(2,-1);
(3) y随x增大而减小时自变量x的取值范围是 .
.
考点:1、二次函数与一元二次方程的关系;2、二次函数的性质.

练习册系列答案
相关题目

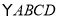 中,
中,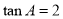 ,
,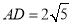 ,
, ,
,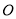 是
是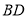 中点,
中点,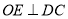 于
于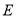 .
.
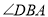 的度数.
的度数. 的面积.
的面积.  的图象分布在第二、四象限,则
的图象分布在第二、四象限,则 的取值范围是______.
的取值范围是______. 是
是 的外接圆,
的外接圆, ,则
,则 的度数为( ).
的度数为( ).
 B.
B. C.
C. D.
D.
 (
( )的图象如图所示,则下列结论:
)的图象如图所示,则下列结论:
 >0; ②b>0; ③
>0; ②b>0; ③ >0;④b2–4
>0;④b2–4 >0,其中正确的个数是 ( )
>0,其中正确的个数是 ( ) ),商家按进价的3倍定价销售了一段时间后,为了吸引顾客,又在原定价的基础上打六折出售,那么按新的售价销售,每件童装所得的利润用代数式表示应为 元.
),商家按进价的3倍定价销售了一段时间后,为了吸引顾客,又在原定价的基础上打六折出售,那么按新的售价销售,每件童装所得的利润用代数式表示应为 元.