题目内容
 如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是
如图,已知⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,若⊙O1的半径为1,⊙O2的半径为3,则图中阴影部分的面积是
- A.4
 -
- π
π - B.4
 -
- π
π - C.8
 -
- π
π - D.8
 -
- π
π
B
分析:首先连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,易求得O1D的长,利用三角函数的知识求得∠O2的度数,继而可求得梯形与扇形的面积,则可求得答案.
解答: 解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,
解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,
∵⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,⊙O1的半径为1,⊙O2的半径为3,
∴四边形AO1DB是矩形,
∴O1A=BD,
∴O1A=1,O2B=3,O1O2=1+3=4,
∴O2D=3-1=2,
∴O1D= =2
=2 ,
,
∴tan∠O2=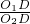 =
= ,
,
∴∠O2=60°,
∴∠AO1O2=180°-∠O2=120°,
∴S梯形ABO2O1= (O1A+O2B)•O1D=
(O1A+O2B)•O1D= ×(1+3)×2
×(1+3)×2 =4
=4 ,S扇形AO1C=
,S扇形AO1C=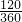 ×π×12=
×π×12= π,S扇形BO2C=
π,S扇形BO2C= ×π×32=
×π×32= π,
π,
∴S阴影=S梯形ABO2O1-S扇形AO1C-S扇形BO2C=4 -
- π.
π.
故选B.
点评:此题考查了相切两圆的性质、梯形的性质、勾股定理以及三角函数的性质.此题难度适中,注意掌握数形结合思想的应用.
分析:首先连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,易求得O1D的长,利用三角函数的知识求得∠O2的度数,继而可求得梯形与扇形的面积,则可求得答案.
解答:
 解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,
解:连接O1A,O2B,O1O2,过点O1作O1D⊥O2B于点D,∵⊙O1与⊙O2外切于点C,AB为两圆外公切线,切点为A,B,⊙O1的半径为1,⊙O2的半径为3,
∴四边形AO1DB是矩形,
∴O1A=BD,
∴O1A=1,O2B=3,O1O2=1+3=4,
∴O2D=3-1=2,
∴O1D=
 =2
=2 ,
,∴tan∠O2=
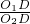 =
= ,
,∴∠O2=60°,
∴∠AO1O2=180°-∠O2=120°,
∴S梯形ABO2O1=
 (O1A+O2B)•O1D=
(O1A+O2B)•O1D= ×(1+3)×2
×(1+3)×2 =4
=4 ,S扇形AO1C=
,S扇形AO1C=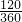 ×π×12=
×π×12= π,S扇形BO2C=
π,S扇形BO2C= ×π×32=
×π×32= π,
π,∴S阴影=S梯形ABO2O1-S扇形AO1C-S扇形BO2C=4
 -
- π.
π.故选B.
点评:此题考查了相切两圆的性质、梯形的性质、勾股定理以及三角函数的性质.此题难度适中,注意掌握数形结合思想的应用.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 24、如图,已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交⊙O1于C、D两点,直线CA交⊙O2于点P,直线PD交⊙O1于点Q,且CP∥QB,求证:AC=AP.
24、如图,已知⊙O1与⊙O2相交于A、B两点,连心线O1O2交⊙O1于C、D两点,直线CA交⊙O2于点P,直线PD交⊙O1于点Q,且CP∥QB,求证:AC=AP.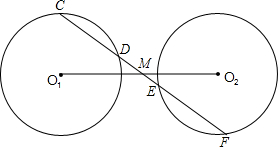 助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母)
助线或另添字母),则M是线段O1O2的中点,并说明理由.(说明理由时可添加辅助线或字母) 如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D.
如图,已知⊙O1与⊙O2相交于A、B两点,过A作⊙O1的切线交⊙O2于E,连接EB并延长交⊙O1于C,直线CA交⊙O2于点D. 如图,已知⊙O1与⊙O2相交于点A、B,AB=8,O1O2=1,⊙O1的半径长为5,那么⊙O2的半径长为
如图,已知⊙O1与⊙O2相交于点A、B,AB=8,O1O2=1,⊙O1的半径长为5,那么⊙O2的半径长为 如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②
如图,已知⊙O1与⊙O2的半径分别为r1,r2,⊙O2经过⊙O1的圆心O1,且两圆相交于A,B两点,C为⊙O2上的点,连接AC交⊙O1于D点,再连接BC,BD,AO1,AO2,O1O2,有如下四个结论:①∠BDC=∠AO1O2;②