题目内容
如图，已知⊙O1与⊙O2相交于点A、B，AB=8，O1O2=1，⊙O1的半径长为5，那么⊙O2的半径长为2
| 5 |
2
．| 5 |
分析：延长O1O2到AB于点E，得出O1E⊥AB于点E，连接AO2，进而利用勾股定理求出即可．
解答：
解：延长O1O2到AB于点E，得出O1E⊥AB于点E，连接AO2，
∵AB=8，∴AE=BE=4，
∵⊙O1的半径长为5，
∴O1E=
=3，
∵O1O2=1，
∴O2E=2，
∴⊙O2的半径长为：
=2
．
故答案为：2
．
解：延长O1O2到AB于点E，得出O1E⊥AB于点E，连接AO2，∵AB=8，∴AE=BE=4，
∵⊙O1的半径长为5，
∴O1E=
| 52-42 |
∵O1O2=1，
∴O2E=2，
∴⊙O2的半径长为：
| 42+22 |
| 5 |
故答案为：2
| 5 |
点评：此题考查了两圆相交的性质，涉及的知识有：勾股定理，以及连心线与公共弦的关系．
练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
新辅教导学系列答案
阳光同学一线名师全优好卷系列答案
相关题目
24、如图，已知⊙O1与⊙O2相交于A、B两点，连心线O1O2交⊙O1于C、D两点，直线CA交⊙O2于点P，直线PD交⊙O1于点Q，且CP∥QB，求证：AC=AP．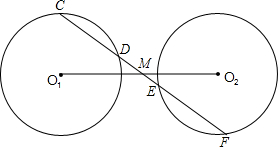
助线或另添字母），则M是线段O1O2的中点，并说明理由．（说明理由时可添加辅助线或字母）
如图，已知⊙O1与⊙O2相交于A、B两点，过A作⊙O1的切线交⊙O2于E，连接EB并延长交⊙O1于C，直线CA交⊙O2于点D．
如图，已知⊙O1与⊙O2的半径分别为r1，r2，⊙O2经过⊙O1的圆心O1，且两圆相交于A，B两点，C为⊙O2上的点，连接AC交⊙O1于D点，再连接BC，BD，AO1，AO2，O1O2，有如下四个结论：①∠BDC=∠AO1O2；②