��Ŀ����
����Ŀ����ͼʾ����������![]() �ĵ�
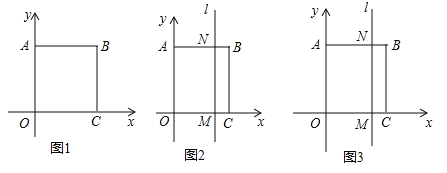
�ĵ�![]() Ϊ����ԭ�㽨��ƽ��ֱ������ϵ�������߶�
Ϊ����ԭ�㽨��ƽ��ֱ������ϵ�������߶�![]() ��
��![]() ���ϣ��߶�
���ϣ��߶�![]() ��
��![]() ���ϣ�����������
���ϣ�����������![]() ���ܳ�Ϊ24��
���ܳ�Ϊ24��
��1��ֱ��д��![]() ��
��![]() ��������꣮
��������꣮
��2������![]() ���غϵ�ֱ��
���غϵ�ֱ��![]() ��ÿ��1����λ���ȵ��ٶ���
��ÿ��1����λ���ȵ��ٶ���![]() ������ƽ�ƣ��ƶ�����
������ƽ�ƣ��ƶ�����![]() ���ڵ�ֱ���غ�ʱֹͣ�����ƶ�������ֱ��
���ڵ�ֱ���غ�ʱֹͣ�����ƶ�������ֱ��![]() ��
��![]() ��
��![]() ����ֱ�Ϊ��
����ֱ�Ϊ��![]() �͵�
�͵�![]() ���ʣ��˶��ʱ��ʱ��������
���ʣ��˶��ʱ��ʱ��������![]() ���ܳ��볤����
���ܳ��볤����![]() ���ܳ�֮��Ϊ5��4��
���ܳ�֮��Ϊ5��4��
��3���ڣ�2���������£���ֱ��![]() ����һ��
����һ��![]() ������
������![]() ��
��![]() ��ǡ������
��ǡ������![]() �����
�����![]() �Ĵ�С��
�Ĵ�С��
���𰸡���1��B��6,6����C��6,0������2���˶�4��ʱ��������![]() ���ܳ��볤����
���ܳ��볤����![]() ���ܳ�֮��Ϊ5��4����3��
���ܳ�֮��Ϊ5��4����3��![]() Ϊ270����90��ʱǡ��
Ϊ270����90��ʱǡ��![]() .
.
��������
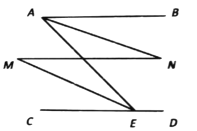
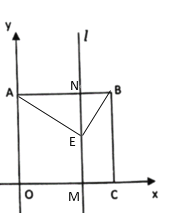
��1�����������ε����ʼ��ɵõ�OA��OC�ij����ɴ˵õ�������ꣻ
��2�����ƶ�t�룬����ƽ�Ƶõ�AN=OM=t��MN=OA=6�����ݳ�����![]() ���ܳ��볤����
���ܳ��볤����![]() ���ܳ�֮��Ϊ5��4�г�������⼴�ɵõ��𰸣�
���ܳ�֮��Ϊ5��4�г�������⼴�ɵõ��𰸣�
��3���������������E��AB�Ϸ����·�ʱ���ֱ�ͼ�����ݴ�ֱ�Ķ��弰�����ε�������ֵ����.
��1�����ı���ABCO�������Σ����ܳ���24��
��OA=OC=AB=BC=6��AB��OA��BC��OC��
��B��6,6����C��6,0����
��2�����ƶ�t�룬
����![]() ���غϵ�ֱ��
���غϵ�ֱ��![]() ��ÿ��1����λ���ȵ��ٶ���
��ÿ��1����λ���ȵ��ٶ���![]() ������ƽ�ƣ�
������ƽ�ƣ�
��AN=OM=t��MN=OA=6��
��BN=CM=6-t��
�߳�����![]() ���ܳ��볤����
���ܳ��볤����![]() ���ܳ�֮��Ϊ5��4��
���ܳ�֮��Ϊ5��4��
��4��2t+12��=5��12-2t+12����
���t=4��
�൱ֱ��l�˶�4��ʱ��������![]() ���ܳ��볤����
���ܳ��볤����![]() ���ܳ�֮��Ϊ5��4��
���ܳ�֮��Ϊ5��4��
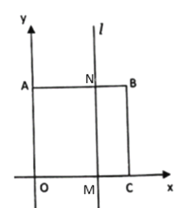
��3������E��AB�Ϸ�ʱ����ͼ��
��![]() ��
��
���AEB=90����
���EAB+��EBA=90����
���ı���ABCO�������Σ�
���OAB=��ABC=90����
��![]() =��OAB+��EAB+��ABC+��EBA=270����
=��OAB+��EAB+��ABC+��EBA=270����
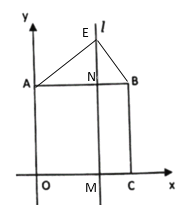
����E��AB�·�ʱ����ͼ��
��![]() ��
��
���AEB=90����
���EAB+��EBA=90����
���ı���ABCO�������Σ�
���OAB=��ABC=90����
��![]() =��OAB-��EAB+��ABC-��EBA=90����
=��OAB-��EAB+��ABC-��EBA=90����
���ϣ�![]() Ϊ270����90��ʱǡ��
Ϊ270����90��ʱǡ��![]() .
.

 �ŵ������ϵ�д�
�ŵ������ϵ�д�