题目内容
试求所有的这样的四位数:它们都是自己各位数字之和的83倍.
【答案】分析:可设四位数为abcd(a不等于0),则有1000a+100b+10c+d=83(a+b+c+d),可得917a+17b-73c-82d=0,从而得到a=1,再找到在1000-2000中是83倍数的数,找到符合题意的四位数即可.
解答:解:设四位数为abcd(a不等于0),则有
1000a+100b+10c+d=83(a+b+c+d),
得917a+17b-73c-82d=0
根据等式结构,得a=1,
若a≥2,就算c,d都取最大值9,左边仍然>0
而在1000-2000中是83倍数的只有:
1079,1162,1245,1328,1411,1494,1577,1660,1743,1826,1909,1992.
经检验得,只有1494符合题意.
点评:考查了数的整除性,本题关键是得到四位数千位上面的数字为1.
解答:解:设四位数为abcd(a不等于0),则有
1000a+100b+10c+d=83(a+b+c+d),
得917a+17b-73c-82d=0
根据等式结构,得a=1,
若a≥2,就算c,d都取最大值9,左边仍然>0
而在1000-2000中是83倍数的只有:
1079,1162,1245,1328,1411,1494,1577,1660,1743,1826,1909,1992.
经检验得,只有1494符合题意.
点评:考查了数的整除性,本题关键是得到四位数千位上面的数字为1.

练习册系列答案
相关题目
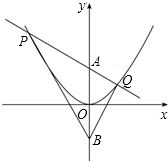 于P,Q两点.
于P,Q两点. (2011•庆阳)如图,抛物线C1:y=x2+2x-3的顶点为M,与x轴相交于A、B两点,与y轴交于点D;抛物线C2与抛物线C1关于y轴对称,顶点为N,与x轴相交于E、F两点.
(2011•庆阳)如图,抛物线C1:y=x2+2x-3的顶点为M,与x轴相交于A、B两点,与y轴交于点D;抛物线C2与抛物线C1关于y轴对称,顶点为N,与x轴相交于E、F两点. 如图,抛物线C1:y=x2+2x-3的顶点为M,与x轴相交于A、B两点,与y轴交于点D;抛物线C2与抛物线C1关于y轴对称,顶点为N,与x轴相交于E、F两点.
如图,抛物线C1:y=x2+2x-3的顶点为M,与x轴相交于A、B两点,与y轴交于点D;抛物线C2与抛物线C1关于y轴对称,顶点为N,与x轴相交于E、F两点.
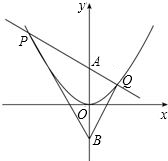 于P,Q两点.
于P,Q两点.