题目内容
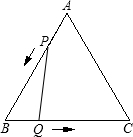 已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?
已知:如图,△ABC是边长3cm的等边三角形,动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为t(s),解答问题:当t为何值时,△PBQ是直角三角形?
分析:本题涉及的是一道有关等边三角形的性质和勾股定理来解答的数形结合试题,根据等边三角形的性质可以知道这个直角三角形∠B=60°,所以就可以表示出BQ与PB的关系,要分情况进行讨论:①∠BPQ=90°;②∠BQP=90°.然后在直角三角形BQP中根据BP,BQ的表达式和∠B的度数进行求解即可.
解答:解:根据题意得AP=tcm,BQ=tcm,
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3-t)cm,
△PBQ中,BP=3-t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=
BP,
即t=
(3-t),t=1(秒),
当∠BPQ=90°时,BP=
BQ,
3-t=
t,t=2(秒).
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
△ABC中,AB=BC=3cm,∠B=60°,
∴BP=(3-t)cm,
△PBQ中,BP=3-t,BQ=t,若△PBQ是直角三角形,则
∠BQP=90°或∠BPQ=90°,
当∠BQP=90°时,BQ=
| 1 |
| 2 |
即t=
| 1 |
| 2 |
当∠BPQ=90°时,BP=
| 1 |
| 2 |
3-t=
| 1 |
| 2 |
答:当t=1秒或t=2秒时,△PBQ是直角三角形.
点评:本题主要考查了直角三角形的判定、勾股定理等知识点.考查学生数形结合的数学思想方法.

练习册系列答案
相关题目
 17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N.
17、已知,如图,△ABC中,∠BAC=90°,AD⊥BC于点D,BE平分∠ABC,交AD于点M,AN平分∠DAC,交BC于点N. 已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长.
已知:如图,∠ABC、∠ACB 的平分线相交于点F,过F作DE∥BC于D,交AC 于E,且AB=6,AC=5,求三角形ADE的周长. 已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE.
已知:如图,△ABC是等边三角形,点D在AB上,点E在AC的延长线上,且BD=CE,DE交BC于F,求证:BF=CF+CE. 已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A.
已知:如图,△ABC中,AB=AC=10,BC=16,点D在BC上,DA⊥CA于A. 已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.
已知:如图,△ABC中,AD⊥BC,BD=DE,点E在AC的垂直平分线上.