题目内容
如图,在平面直角坐标系中,已知抛物线y=ax2+bx的对称轴为x= ,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
,且经过点A(2,1),点P是抛物线上的动点,P的横坐标为m(0<m<2),过点P作PB⊥x轴,垂足为B,PB交OA于点C,点O关于直线PB的对称点为D,连接CD,AD,过点A作AE⊥x轴,垂足为E.
(1)求抛物线的解析式;
(2)填空:
①用含m的式子表示点C,D的坐标:
C( , ),D( , );
②当m= 时,△ACD的周长最小;
(3)若△ACD为等腰三角形,求出所有符合条件的点P的坐标.

解:(1)依题意,得 ,解得
,解得
∴y=x2﹣ x
x
(2)C(m, m),D(2m,0),m=1
m),D(2m,0),m=1
(3)依题意,得B(m,0)
在RT△OBC中,OC2=OB2+BC2=m2+ =
= m2,
m2,
∴OC= m 又∵O,D关于直线PC对称,
m 又∵O,D关于直线PC对称,
∴CD=OC= m
m
在RT△AOE中,OA= =
= =
=
∴AC=OA﹣OC= ﹣
﹣ m
m
在RT△ADE中,AD2=AE 2+DE2=12+(2﹣2m)2=4m2﹣8m+5
2+DE2=12+(2﹣2m)2=4m2﹣8m+5
分三种情况讨论:
①若AC=CD,即 ﹣
﹣ m=
m= m,解得m=1,∴P(1,
m,解得m=1,∴P(1, )
)
②若AC=AD,则有AC2=AD2,即5﹣5m+ m2=4m2﹣8m+5
m2=4m2﹣8m+5
解得m1=0,m2= .∵0<m<2,∴m=
.∵0<m<2,∴m= ,∴P(
,∴P( ,
, )
)
③若DA=DC,则有D A2=DC2,即4m2﹣8m+5=
A2=DC2,即4m2﹣8m+5= m2
m2
解得m1= ,m2=2,∵,0<m<2,∴m=
,m2=2,∵,0<m<2,∴m= ,∴P(
,∴P( ,
, )
)
综上所述,当△ACD为等腰三角形是,点P的坐标分别为P1(1, ),P2(
),P2( ,
, ),P3(
),P3( ,
, ).
).

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 图2
图2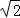 ≈1.414,
≈1.414,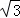 ≈1.732)
≈1.732)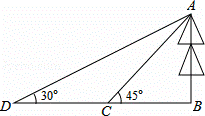
 =
= .
. B.
B.  C.
C.  D.
D. 
 中,AB∥CD,
中,AB∥CD, ,
, .取
.取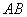 的中点
的中点 ,连接
,连接 ,再分别取
,再分别取 的中点
的中点 ,
, ,连接
,连接 ,得到四边形
,得到四边形 ,如图2;同样方法操作得到四边形
,如图2;同样方法操作得到四边形 ,如图3;…,如此进行下去,则四边形
,如图3;…,如此进行下去,则四边形 的面积为 .
的面积为 . 