题目内容
【题目】如图，人工喷泉有一个竖直的喷水枪AB，喷水口A距地面2.25m，喷出水流的运动路线是抛物线．水流的最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3m．求水流的落地点C到水枪底部B的距离．
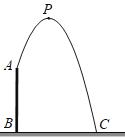
【答案】水流的落地点C到水枪底部B的距离为3m．
【解析】
如图，以点B为原点，AB为y轴，BC为x轴建立平面直角坐标系，根据点P到x轴、y轴的距离可得点P坐标，设抛物线的解析式为y＝a（x﹣1）2+3，把A点坐标代入可求出a值，可得抛物线的解析式，把y=0代入求出x的值即可得答案.
如图，以点B为原点，AB为y轴，BC为x轴建立平面直角坐标系
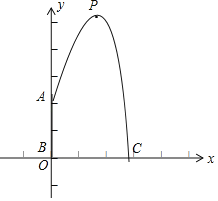
∵最高点P到喷水枪AB所在直线的距离为1m，且到地面的距离为3m．
∴抛物线的顶点P（1，3）
∴设抛物线的解析式为y＝a（x﹣1）2+3，
∵A（0，2.25）
∴a(0-1)2+3=2.25，
解得：a＝﹣0.75
∴y＝﹣0.75（x﹣1）2+3
令y＝0
﹣0.75（x﹣1）2+3＝0
解得x1＝3，x2＝﹣1（舍）
∴BC＝3．
答：水流的落地点C到水枪底部B的距离为3m．
练习册系列答案
周周清检测系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
