题目内容
已知二次函数的y=ax2+bx+c图象是由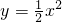 的图象经过平移而得到,若图象与x轴交于A、C(-1,0)两点,与y轴交于D(0,
的图象经过平移而得到,若图象与x轴交于A、C(-1,0)两点,与y轴交于D(0, ),顶点为B,则四边形ABCD的面积为
),顶点为B,则四边形ABCD的面积为
- A.9
- B.10
- C.11
- D.12
A
分析:由题意先得a= ,然后把C(-1,0),D(0,
,然后把C(-1,0),D(0, )代入解析式得到b=3,则y=
)代入解析式得到b=3,则y= x2+3x+
x2+3x+ ;令y=0,得,
;令y=0,得, x2+3x+
x2+3x+ =0,得点坐标为(-5,0),AC=-1-(-5)=4;计算-
=0,得点坐标为(-5,0),AC=-1-(-5)=4;计算- =-3,
=-3, =-2,得到顶点B的坐标为(-3,-2),所以S四边形ABCD=S△ACB+S△ACD,
=-2,得到顶点B的坐标为(-3,-2),所以S四边形ABCD=S△ACB+S△ACD,
即可得到四边形ABCD的面积.
解答:由题意得,a= ,
,
∴y= x2+bx+c,
x2+bx+c,
又∵抛物线过C(-1,0),D(0, ),
),
∴ -b+c=0,c=
-b+c=0,c= ,
,
∴b=3,
∴y= x2+3x+
x2+3x+ ;
;
则- =-3,
=-3, =-2,所以顶点B的坐标为(-3,-2),
=-2,所以顶点B的坐标为(-3,-2),
令y=0,得, x2+3x+
x2+3x+ =0,解得x1=-1,x2=-5,则A点坐标为(-5,0),AC=-1-(-5)=4;
=0,解得x1=-1,x2=-5,则A点坐标为(-5,0),AC=-1-(-5)=4;
如图

S四边形ABCD=S△ACB+S△ACD= ×4×2+
×4×2+ ×4×
×4× =9.
=9.
故选A.
点评:本题考查了用待定系数法求抛物线的解析式,二次函数的一般式:y=ax2+bx+c(a≠0).同时考查了求抛物线与x轴交点坐标的方法以及顶点的坐标;考查了在坐标系中求几何图形面积的方法.
分析:由题意先得a=
 ,然后把C(-1,0),D(0,
,然后把C(-1,0),D(0, )代入解析式得到b=3,则y=
)代入解析式得到b=3,则y= x2+3x+
x2+3x+ ;令y=0,得,
;令y=0,得, x2+3x+
x2+3x+ =0,得点坐标为(-5,0),AC=-1-(-5)=4;计算-
=0,得点坐标为(-5,0),AC=-1-(-5)=4;计算- =-3,
=-3, =-2,得到顶点B的坐标为(-3,-2),所以S四边形ABCD=S△ACB+S△ACD,
=-2,得到顶点B的坐标为(-3,-2),所以S四边形ABCD=S△ACB+S△ACD,即可得到四边形ABCD的面积.
解答:由题意得,a=
 ,
,∴y=
 x2+bx+c,
x2+bx+c,又∵抛物线过C(-1,0),D(0,
 ),
),∴
 -b+c=0,c=
-b+c=0,c= ,
,∴b=3,
∴y=
 x2+3x+
x2+3x+ ;
;则-
 =-3,
=-3, =-2,所以顶点B的坐标为(-3,-2),
=-2,所以顶点B的坐标为(-3,-2),令y=0,得,
 x2+3x+
x2+3x+ =0,解得x1=-1,x2=-5,则A点坐标为(-5,0),AC=-1-(-5)=4;
=0,解得x1=-1,x2=-5,则A点坐标为(-5,0),AC=-1-(-5)=4;如图

S四边形ABCD=S△ACB+S△ACD=
 ×4×2+
×4×2+ ×4×
×4× =9.
=9.故选A.
点评:本题考查了用待定系数法求抛物线的解析式,二次函数的一般式:y=ax2+bx+c(a≠0).同时考查了求抛物线与x轴交点坐标的方法以及顶点的坐标;考查了在坐标系中求几何图形面积的方法.

练习册系列答案
相关题目
 已知二次函数的图象如右图,则下列结论中,正确的结论有( )
已知二次函数的图象如右图,则下列结论中,正确的结论有( )①a+b+c>0 ②a-b+c<0 ③abc<0 ④b=2a ⑤b>0.
| A、5个 | B、4个 | C、3个 | D、2个 |
已知二次函数的图象经过(1,0)、(2,0)和(0,2)三点,则该函数的解析式是( )
| A、y=2x2+x+2 | B、y=x2+3x+2 | C、y=x2-2x+3 | D、y=x2-3x+2 |
 9、已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )
9、已知二次函数的图象(0≤x≤3)如图所示,关于该函数在所给自变量取值范围内,下列说法正确的是( )