题目内容
如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC，若半径r=2cm，∠BCD=22°30′，则弦AB=考点：垂径定理,等腰直角三角形,圆周角定理
专题：
分析：连接OA、OB，根据圆周角定理求出∠BOD，求出∠AOD=∠BOD=45°，根据勾股定理求出即可．
解答：
解：连接OA、OB，
∵∠BCD=22°30′，
∴∠BOD=2∠BCD=45°，
∵在⊙O中，CD是直径，弦AB⊥CD，
∴弧AD=弧BD，
∴∠AOD=∠BOD=45°，
∴∠AOB=90°，
由勾股定理得：AB=
=
=2
，
故答案为：2
．
解：连接OA、OB，∵∠BCD=22°30′，
∴∠BOD=2∠BCD=45°，
∵在⊙O中，CD是直径，弦AB⊥CD，
∴弧AD=弧BD，
∴∠AOD=∠BOD=45°，
∴∠AOB=90°，
由勾股定理得：AB=
| AO2+BO2 |
| 22+22 |
| 2 |
故答案为：2
| 2 |
点评：本题考查了垂径定理，勾股定理，圆周角定理的应用，解此题的关键是求出∠AOB的度数，题目比较好，难度适中．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
新活力总动员暑系列答案
相关题目
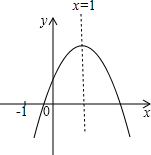已知二次函数y=ax2+bx+c的图象如图所示，下列结论：①abc＞0；②a+c＞b；③4a+2b+c＞0；④2a+b=0；⑤b2-4ac＞0
其中正确的结论有（ ）
| A、2个 | B、3个 | C、4个 | D、5个 |
AD是△ABC的角平分线，作DE⊥AB于E，DF⊥AC于F，下列结论错误的是（ ）
| A、DE=DF |
| B、AE=AF |
| C、BD=CD |
| D、∠ADE=∠ADF |
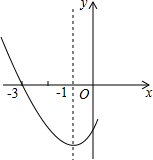如图是二次函数y=ax2+bx+c图象的一部分，其对称轴是x=-1，且过点（-3，0），下列说法：①abc＜0；②2a-b=0；③4a+2b+c＜0；④若（-5，y1），（