题目内容
【题目】已知：如图，△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：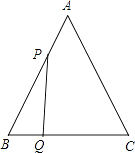 
（1）经过 
秒时，求△PBQ的面积；
（2）当t为何值时，△PBQ是直角三角形？
（3）是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出t的值；不存在请说明理由．
【答案】
（1）解：经过 
秒时，AP= cm，BQ= cm，
∵△ABC是边长为3cm的等边三角形，
∴AB=BC=3cm，∠B=60°，
∴BP=3﹣ = 
cm，
∴△PBQ的面积= 
BPBQsin∠B= × × × 
= 
（2）解：设经过t秒△PBQ是直角三角形，
则AP=tcm，BQ=tcm，
△ABC中，AB=BC=3cm，∠B=60°，
∴BP=（3﹣t）cm，
△PBQ中，BP=（3﹣t）cm，BQ=tcm，若△PBQ是直角三角形，则∠BQP=90°或∠BPQ=90°，
当∠BQP=90°时，BQ= BP，
即t= （3﹣t），t=1（秒），
当∠BPQ=90°时，BP= BQ，
3﹣t= t，t=2（秒），
答：当t=1秒或t=2秒时，△PBQ是直角三角形
（3）解：过P作PM⊥BC于M，
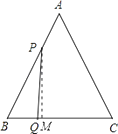
△BPM中，sin∠B= 
，
∴PM=PBsin∠B= （3﹣t），
∴S△PBQ= BQPM= t （3﹣t），
∴y=S△ABC﹣S△PBQ= ×32× ﹣ ×t× 
（3﹣t）
= 
t2﹣ 
t+ 
，
∴y与t的关系式为y= t2﹣ t+ ，
假设存在某一时刻t，使得四边形APQC的面积是△ABC面积的 
，
则S四边形APQC= S△ABC，
∴ t2﹣ t+ = × ×32× ，
∴t2﹣3t+3=0，
∵（﹣3）2﹣4×1×3＜0，
∴方程无解，
∴无论t取何值，四边形APQC的面积都不可能是△ABC面积的 ．
【解析】（1）根据路程=速度×时间，求出BQ，AP的值，再求出BP的值，然后利用三角形的面积公式进行解答即可；（2）①∠BPQ=90°；②∠BQP=90°．然后在直角三角形BQP中根据BP，BQ的表达式和∠B的度数进行求解即可．（3）本题可先用△ABC的面积﹣△PBQ的面积表示出四边形APQC的面积，即可得出y，t的函数关系式，然后另y等于三角形ABC面积的三分之二，可得出一个关于t的方程，如果方程无解则说明不存在这样的t值，如果方程有解，那么求出的t值即可
