题目内容
 如图,D是等腰三解形△ABC(AB=BC)的外角平分线上的一点,DC⊥BC,∠ABC=120°,若BD=2,则△ABD的面积为
如图,D是等腰三解形△ABC(AB=BC)的外角平分线上的一点,DC⊥BC,∠ABC=120°,若BD=2,则△ABD的面积为
- A.2
- B.3
- C.

- D.

C
分析:过D作DE⊥AB于E,根据邻补角定义求出∠CBE=60°,再根据角平分线的定义求出∠CBD=30°,然后根据30°角所对的直角边等于斜边的一半求出CD,利用勾股定理列式求出BC,从而得到AB的长度,再根据角平分线上的点到角的两边的距离相等可得DE=CD,然后利用三角形的面积公式列式进行计算即可得解.
解答: 解:如图,过D作DE⊥AB于E,
解:如图,过D作DE⊥AB于E,
∵∠ABC=120°,
∴∠CBE=180°-120°=60°,
∵BD是△ABC的外角平分线,
∴∠CBD= ×60°=30°,
×60°=30°,
∴CD= BD=
BD= ×2=1,
×2=1,
∵DC⊥BC,
∴BC=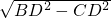 =
= =
= ,
,
∴AB=BC= ,
,
∵BD是△ABC的外角平分线,DC⊥BC,
∴DE=CD=1,
∴△ABD的面积= ×
× ×1=
×1= .
.
故选C.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,勾股定理的应用,熟记性质并作出辅助线得到AB边上的高是解题的关键.
分析:过D作DE⊥AB于E,根据邻补角定义求出∠CBE=60°,再根据角平分线的定义求出∠CBD=30°,然后根据30°角所对的直角边等于斜边的一半求出CD,利用勾股定理列式求出BC,从而得到AB的长度,再根据角平分线上的点到角的两边的距离相等可得DE=CD,然后利用三角形的面积公式列式进行计算即可得解.
解答:
 解:如图,过D作DE⊥AB于E,
解:如图,过D作DE⊥AB于E,∵∠ABC=120°,
∴∠CBE=180°-120°=60°,
∵BD是△ABC的外角平分线,
∴∠CBD=
 ×60°=30°,
×60°=30°,∴CD=
 BD=
BD= ×2=1,
×2=1,∵DC⊥BC,
∴BC=
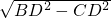 =
= =
= ,
,∴AB=BC=
 ,
,∵BD是△ABC的外角平分线,DC⊥BC,
∴DE=CD=1,
∴△ABD的面积=
 ×
× ×1=
×1= .
.故选C.
点评:本题考查了角平分线上的点到角的两边的距离相等的性质,勾股定理的应用,熟记性质并作出辅助线得到AB边上的高是解题的关键.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目
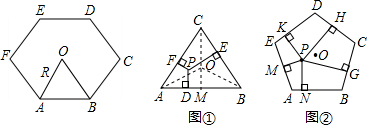 (2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
(2012•青岛模拟)同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系? 如图,D是等腰三解形△ABC(AB=BC)的外角平分线上的一点,DC⊥BC,∠ABC=120°,若BD=2,则△ABD的面积为( )
如图,D是等腰三解形△ABC(AB=BC)的外角平分线上的一点,DC⊥BC,∠ABC=120°,若BD=2,则△ABD的面积为( )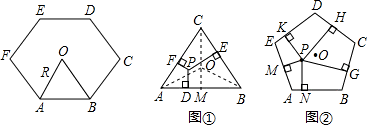 同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?
同学们已经认识了很多正多边形,现以正六边形为例再介绍与正多边形相关的几个概念.如正六边形ABCDEF各边对称轴的交点O,又称正六边形的中心,其中OA称正六边形的半径,通常用R表示,∠AOB称为中心角,显然.提出问题:正多边形内任意一点到各边距离之和与这个正多边形的半径R和中心角有什么关系?