题目内容
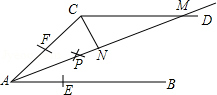
如图1,两条射线AP、AQ交于点A,B点在AP上,C点在AQ上,连接CB并延长.
(1)作∠ACB和∠ABD的平分线交于点M,探索∠M与∠A的关系;
(2)如图2,作∠PBC和∠BCQ的平分线交于点N,问当B点和C点在AP和AQ上运动的时候,∠M+∠N的度数和会如何变化?并给出理由.
(3)当∠A的大小在大于0°小于90°间变化时,∠M+∠N的度数变化吗?如果变化请写出∠M+∠N的变化范围.

 解:(1)∵在△ABC中,∠ABD=∠A+∠ACB,
解:(1)∵在△ABC中,∠ABD=∠A+∠ACB,又∠1=∠2,∠3=∠4,
∴2∠1=∠A+2∠3,
又在△BCM中,∠1=∠M+∠3,
∴∠A=2∠M;
(2)∵∠PBC=∠A+∠ACB,
∠BCQ=∠A+∠ABC,
∴∠PBC+∠PCQ=∠A+∠ACB+∠ABC+∠A=180°+∠A,
又∵BN、CN是∠PBC和∠BCQ的角平分线,即∠NBC=
 ∠PBC,∠BCN=
∠PBC,∠BCN= ∠BCQ,
∠BCQ,∴∠NBC+∠BCN=
 (180°+∠A)=90°-
(180°+∠A)=90°- ∠A,
∠A,∴∠N=180°-(∠NBC+∠BCN)=90°+
 ∠A,
∠A,∴∠M+∠N=
 ∠A-(90°+
∠A-(90°+ ∠A)=90°.
∠A)=90°.故∠M+∠N的度数不变;
(3)根据(2)可以得到∠M+∠N=90°,故∠M+∠N的度数不变.
分析:(1)根据在△ABC中,∠ABD=∠A+∠ACB,以及在△BCM中,∠1=∠M+∠3,即可求解;
(2)根据三角形的外角的性质,可以得到∠PBC+∠PCQ=∠A+∠ACB+∠ABC+∠A=180°+∠A,即可利用∠A表示出∠M,结合(1)的结果即可确定;
(3)与(2)的解法完全相同,直接利用(2)的结果即可说明.
点评:本题考查了三角形的外角的性质,正确证明∠A=2∠M,∠N=90°+
 ∠A是关键.
∠A是关键. 
练习册系列答案
 全程金卷系列答案
全程金卷系列答案
相关题目
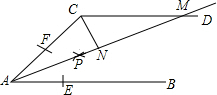 (2012•绍兴)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2012•绍兴)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于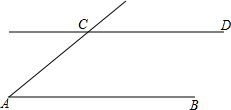 (2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于
(2013•怀集县二模)如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于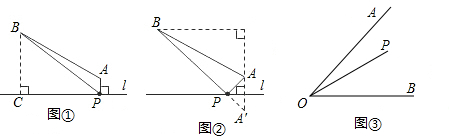
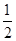 EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。