题目内容
若点(m,n)在一次函数y=2x-8的图象上,先化简,再求值:[(m2+n2)-(m-n)2]÷4n+
(m-n).
| 1 | 2 |
分析:先把原式进行化简,再根据点(m,n)在一次函数y=2x-8的图象上可用m表示出n的值,把n代入代数式进行计算即可.
解答:解:原式=2mn÷4n+
(m-n)
=
m+
m-
n
=m-
n.
∵点(m,n)在一次函数y=2x-8的图象上,
∴n=2m-8,
∴原式=m-
(2m-8)=m-m+4=4.
| 1 |
| 2 |
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=m-
| 1 |
| 2 |
∵点(m,n)在一次函数y=2x-8的图象上,
∴n=2m-8,
∴原式=m-
| 1 |
| 2 |
点评:本题考查的是一次函数图象上点的坐标特征,一次函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
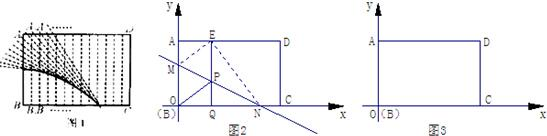
 某特种侦察小队在一次作战行动中发现一个空中固定目标点C,并以O、A为两观察点,分别测得目标C的仰角分别是α和β,且tanα=
某特种侦察小队在一次作战行动中发现一个空中固定目标点C,并以O、A为两观察点,分别测得目标C的仰角分别是α和β,且tanα=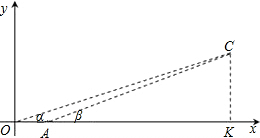

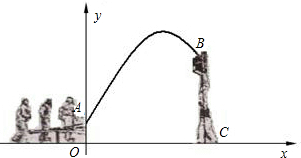 看成一点)的路线是抛物线y=
看成一点)的路线是抛物线y=