题目内容
半径为1的圆中有一条弦,如果它的长为 ,那么这条弦所对的圆周角的度数等于________.
,那么这条弦所对的圆周角的度数等于________.
60°或120°
分析:根据垂径定理求得AD的长,再根据三角形函数可得到∠AOD的度数,再根据圆周角定理得到∠ACB的度数,根据圆内接四边形的对角互补即可求得∠AEB的度数.
解答: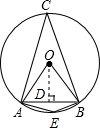 解:过O作OD⊥AB,则AD=
解:过O作OD⊥AB,则AD= AB=
AB= ×
× =
= .
.
∵OA=1,
∴sin∠AOD= =
= ,∠AOD=60°.
,∠AOD=60°.
∵∠AOD= ∠AOB=60°,∠ACB=
∠AOB=60°,∠ACB= ∠AOB,
∠AOB,
∴∠ACB=∠AOD=60°.
又∵四边形AEBC是圆内接四边形,
∴∠AEB=180°-∠ACB=180°-60°=120°.
故这条弦所对的圆周角的度数等于60°或120度.
点评:此题考查圆周角定理,圆内接四边形的性质.在解答此类题目时一定要注意,一条弦所对的圆周角有两个,这两个角互补,不要漏解.
分析:根据垂径定理求得AD的长,再根据三角形函数可得到∠AOD的度数,再根据圆周角定理得到∠ACB的度数,根据圆内接四边形的对角互补即可求得∠AEB的度数.
解答:
 解:过O作OD⊥AB,则AD=
解:过O作OD⊥AB,则AD= AB=
AB= ×
× =
= .
.∵OA=1,
∴sin∠AOD=
 =
= ,∠AOD=60°.
,∠AOD=60°.∵∠AOD=
 ∠AOB=60°,∠ACB=
∠AOB=60°,∠ACB= ∠AOB,
∠AOB,∴∠ACB=∠AOD=60°.
又∵四边形AEBC是圆内接四边形,
∴∠AEB=180°-∠ACB=180°-60°=120°.
故这条弦所对的圆周角的度数等于60°或120度.
点评:此题考查圆周角定理,圆内接四边形的性质.在解答此类题目时一定要注意,一条弦所对的圆周角有两个,这两个角互补,不要漏解.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目