题目内容
已知⊙01与⊙02的半径分别为3和7,圆心距0102=8,则两圆的位置关系是( )
| A、相交 | B、外切 | C、内切 | D、外离 |
考点:圆与圆的位置关系
专题:
分析:求出两圆半径的和与差,再与圆心距比较大小,确定两圆位置关系.根据两圆的位置关系得到其数量关系.
设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.
设两圆的半径分别为R和r,且R≥r,圆心距为d:外离,则d>R+r;外切,则d=R+r;相交,则R-r<d<R+r;内切,则d=R-r;内含,则d<R-r.
解答:解:因为7-3=4,7+3=10,圆心距为8,
所以4<8<10,
根据两圆相交,圆心距的长度在两圆的半径的差与和之间,
所以两圆相交.
故选A.
所以4<8<10,
根据两圆相交,圆心距的长度在两圆的半径的差与和之间,
所以两圆相交.
故选A.
点评:考查了圆与圆的位置关系,本题利用了两圆相交,圆心距的长度在两圆的半径的差与和之间求解.

练习册系列答案
相关题目
下列方程中,属于一元二次方程的是( )
| A、x+y=2 | ||
| B、x2-2y+1=0 | ||
C、2y2-
| ||
D、
|
下列计算正确的是( )
| A、3a-a=2 |
| B、(a2)4=a8 |
| C、a+a4=a5 |
| D、(a+b)(a-b)=a2+b2 |
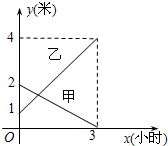 自来水公司有甲、乙两个长方体的蓄水池,现将甲池中的水以每小时8m3的速度注入乙池,则两水池中水的高度y(m)与注水的时间x(h)之间的函数图象如图所示.若要乙池的蓄水量是甲池的2倍,则注水的时间应为( )
自来水公司有甲、乙两个长方体的蓄水池,现将甲池中的水以每小时8m3的速度注入乙池,则两水池中水的高度y(m)与注水的时间x(h)之间的函数图象如图所示.若要乙池的蓄水量是甲池的2倍,则注水的时间应为( )| A、2h | ||
B、
| ||
C、
| ||
D、
|
在相同条件下重复试验,若事件A发生的概率是
,下列陈述正确的是( )
| 7 |
| 100 |
| A、说明做100次这种试验,事件A必发生7次 | ||
| B、说明大量反复做这种试验,事件A平均每100次发生7次 | ||
| C、说明做100次这种试验,事件A不可能必发生6次 | ||
D、说明事件A发生的频率是
|
在数4,-1,3,-6中,其中最小的是( )
| A、-6 | B、-4 | C、-1 | D、6 |
若
的算术平方根有意义,则a的取值范围是( )
| a |
| A、一切数 | B、正数 |
| C、非负数 | D、非零数 |
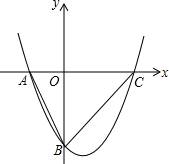 如图,抛物线y=
如图,抛物线y=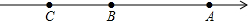 如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=
如图所示,数轴上有A、B、C三点,点B恰好在原点,点A表示的数是9,AC表示数轴上点A与点C两点的距离,BC表示数轴上点B与点C两点的距离,且AB=