题目内容
 如图,长方体中AB=BB′=2,AD=3,一只蚂蚁从A点出发,在长方体表面爬到C′点,求蚂蚁怎样走最短,最短路径是多少?
如图,长方体中AB=BB′=2,AD=3,一只蚂蚁从A点出发,在长方体表面爬到C′点,求蚂蚁怎样走最短,最短路径是多少?
分析:要求蚂蚁爬行的最短距离,需将长方体中的侧面展开,进而根据“两点之间线段最短”得出结果.
解答:解:①如图1,把长方体沿虚线剪开,则成长方形ACC′A′,宽为AA′=2,长为AD+DC=5,
连接AC′则A、D、C′构成直角三角形,由勾股定理得
AC′=
=
=
,

②如图2,把长方体沿虚线剪开,则成长方形ADC′B′,宽为AD=2,长为DD′+D′C′=4,
连接AC′则A、D、C′构成直角三角形,同理,由勾股定理得AC′=5,
∴最短路径是5.

连接AC′则A、D、C′构成直角三角形,由勾股定理得
AC′=
| (AD+CD)2+DD′2 |
| 52+22 |
| 29 |

②如图2,把长方体沿虚线剪开,则成长方形ADC′B′,宽为AD=2,长为DD′+D′C′=4,
连接AC′则A、D、C′构成直角三角形,同理,由勾股定理得AC′=5,
∴最短路径是5.

点评:长方体中的侧面展开图是一个长方形,本题就是把长方体的侧面展开成长方形,“化曲面为平面”,用勾股定理解决.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
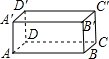 如图,长方体中,AB=12m,BC=2m,BB′=3m,一只蚂蚁从点A出发,以4cm/秒的速度沿长方体表面爬行到点C′,至少需要
如图,长方体中,AB=12m,BC=2m,BB′=3m,一只蚂蚁从点A出发,以4cm/秒的速度沿长方体表面爬行到点C′,至少需要

 如图,长方体中AB=BB′=2,AD=3,一只蚂蚁从A点出发,在长方体表面爬到C′点,求蚂蚁怎样走最短,最短路径是多少?
如图,长方体中AB=BB′=2,AD=3,一只蚂蚁从A点出发,在长方体表面爬到C′点,求蚂蚁怎样走最短,最短路径是多少?