题目内容
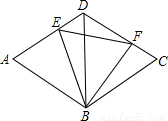
如图，已知D为等边三角形纸片ABC的边AB上的点，过点D作DG∥BC交AC于点G，DE⊥BC于点E，过点G作GF⊥BC于点F．把三角形纸片ABC分别沿DG，DE，GF按图示方式折叠，则图中阴影部分是等边
等边
三角形．分析：根据折叠的性质得到需要判定的三角形的两个角为60°，从而利用三角形内角和定理得到第三个角也为60°，利用三个角都相等的三角形是等边三角形判定即可．
解答：
解：∵三角形ABC为等边三角形，
∴∠A=∠B=∠C=60°，
∵根据题意知道点B和点C经过折叠后分别落在了点I和点H处，
∴∠DIH=∠B=60°，∠GHI=∠C=60°，
∴∠HJI=60°，
∴∠DIH=∠GHI=∠HJI=60°，
∴阴影部分是等边三角形，
故答案为：等边．
解：∵三角形ABC为等边三角形，∴∠A=∠B=∠C=60°，
∵根据题意知道点B和点C经过折叠后分别落在了点I和点H处，
∴∠DIH=∠B=60°，∠GHI=∠C=60°，
∴∠HJI=60°，
∴∠DIH=∠GHI=∠HJI=60°，
∴阴影部分是等边三角形，
故答案为：等边．
点评：本题考查了等边三角形的判定与性质，能熟知“三个角都相等的三角形是等边三角形”是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
