题目内容
17、有n个形状大小都相同的小正方体叠放在一堆后,有如下三视图,则n等于

6
.
分析:由俯视图可得几何体最底层正方体的个数及正方体摆放的形状,按照正视图可得第二层最多有3个正方体,第3层最多有2个正方体,由左视图可得应把正视图得到第二层和第3层正方体的个数各减去1个,把正方体的个数相加即可.
解答:解:∵俯视图中有3个正方形,
∴组合几何体最底层有3个正方体,
∵由正视图可得第二层最多有3个正方体,第3层最多有2个正方体,
由左视图可得应把正视图得到第二层和第3层正方体的个数各减去1个,
∴组合几何体第2层有2个正方体,第三层有1个正方体,
∴组合几何体共有3+2+1=6个正方体.
故答案为:6.
∴组合几何体最底层有3个正方体,
∵由正视图可得第二层最多有3个正方体,第3层最多有2个正方体,
由左视图可得应把正视图得到第二层和第3层正方体的个数各减去1个,
∴组合几何体第2层有2个正方体,第三层有1个正方体,
∴组合几何体共有3+2+1=6个正方体.
故答案为:6.
点评:考查由视图判断几何体;用到的知识点为:“俯视图打地基,正视图疯狂盖,左视图拆违章”.

练习册系列答案
相关题目
 两张卡片.
两张卡片.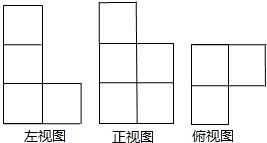 有n个形状大小都相同的小正方体叠放在一堆后,有如下三视图,则n等于________.
有n个形状大小都相同的小正方体叠放在一堆后,有如下三视图,则n等于________. ,
,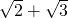 ,
, 三个式子,从中任取
三个式子,从中任取 两张卡片.
两张卡片. ,
, ,
, 三个式子,从中任取两张卡片.
三个式子,从中任取两张卡片.