题目内容
如图,已知直线AB∥CD∥EF,∠POQ=90°,它的顶点O在CD上,两边分别与AB、EF相交于点P,点Q,射线OC 始终在∠POQ的内部.
始终在∠POQ的内部.
(1)求∠1+∠2的度数;
(2)直接写出∠3与∠4的数量关系:
(3)若∠POQ的度数为α,且0°<α<180°,其余条件不变,则∠3与∠4的数量关系为
 始终在∠POQ的内部.
始终在∠POQ的内部.(1)求∠1+∠2的度数;
(2)直接写出∠3与∠4的数量关系:
270°
270°
.(3)若∠POQ的度数为α,且0°<α<180°,其余条件不变,则∠3与∠4的数量关系为
∠3+∠4=360°-α
∠3+∠4=360°-α
.(用含α的式子表示)分析:(1)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2的度数;
(2)由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由(1)求出的∠1+∠2的度数即可得到∠3+∠4的度数;
(3)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2=α,由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由∠1+∠2=α即可得到∠3+∠4的度数.
(2)由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由(1)求出的∠1+∠2的度数即可得到∠3+∠4的度数;
(3)由AB与CD平行,利用两直线平行得到一对内错角相等,由CD与EF平行,同理得到一对内错角相等,而∠POQ=∠POC+∠QOC=90°,等量代换即可求出∠1+∠2=α,由∠APB与∠EQF为两个平角,得到∠1+∠3+∠4+∠2=360°,由∠1+∠2=α即可得到∠3+∠4的度数.
解答:解:(1)∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=90°,
∴∠1+∠2=90°;
(2)∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=90°,
∴∠3+∠4=270°;
(3))∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=α,
∴∠1+∠2=α;
(2)∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=α,
∴∠3+∠4=360°-α.
故答案为:(2)270°;(3)∠3+∠4=360°-α.
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=90°,
∴∠1+∠2=90°;
(2)∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=90°,
∴∠3+∠4=270°;
(3))∵AB∥CD,
∴∠1=∠POC,
∵CD∥EF,
∴∠2=∠QOC,
∵∠POQ=∠POC+∠QOC=α,
∴∠1+∠2=α;
(2)∵∠1+∠3=180°,∠4+∠2=180°,
∴∠1+∠3+∠4+∠2=360°,
又∵∠1+∠2=α,
∴∠3+∠4=360°-α.
故答案为:(2)270°;(3)∠3+∠4=360°-α.
点评:此题考查了平行线的性质,利用了等量代换的思想,熟练掌握平行线的性质是解本题的关键.

练习册系列答案
相关题目
 13、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于
13、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=70°,则∠BOD的度数等于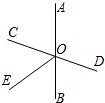 15、如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=50°,那么∠AOC=
15、如图,已知直线AB、CD相交于点O,OE平分∠BOC,如果∠BOE=50°,那么∠AOC=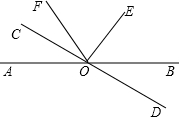 如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数.
如图,已知直线AB和CD相交于O点,∠DOE是直角,OF平分∠AOE,∠BOD=22°,求∠COF的度数. 如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF.
如图,已知直线AB∥CD,∠A=∠C=100°,E、F在CD上,且满足∠DBF=∠ABD,BE平分∠CBF. 如图,已知直线AB∥CD,EM⊥FM,∠MFD=25°,求∠MEB的度数.
如图,已知直线AB∥CD,EM⊥FM,∠MFD=25°,求∠MEB的度数.