题目内容
 如图,直线y=kx交双曲线y=-
如图,直线y=kx交双曲线y=-| 3 | x |
分析:此题可设直线y=-x平移后的表达式为y=-x+b,则C点坐标(b,0),又直线y=kx、直线y=-x+b与 y=-
交于同一点,可得k与b的关系,又OA=OB,可得AB2-4•OC2=4(OA2-OC2),然后再求解.
| 3 |
| x |
解答:解:设直线y=-x平移后的表达式为y=-x+b,则C点坐标(b,0),
由于A在双曲线 y=-
上,则A(x,
),
将A代入y=kx,y=-x+b可得:
,
整理可得:-
=
,
则AB2-4•OC2=4(OA2-OC2)=4(x2+
-b2)=4[-
-3k+
]=4×6=24.
故答案为:24.
由于A在双曲线 y=-
| 3 |
| x |
| -3 |
| x |
将A代入y=kx,y=-x+b可得:
|
整理可得:-
| 3 |
| k |
| b2 |
| (k+1)2 |
则AB2-4•OC2=4(OA2-OC2)=4(x2+
| 9 |
| x2 |
| 3 |
| k |
| 3(k+1)2 |
| k |
故答案为:24.
点评:本题考查了反比例函数的综合应用,由点的坐标写出代数式最后消去k、b是本题的基本思路.

练习册系列答案
相关题目
 如图,直线y=kx交双曲线
如图,直线y=kx交双曲线 如图,直线y=kx交双曲线
如图,直线y=kx交双曲线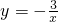 于A、B两点,将直线y=-x平移至经过点A,交x轴于C点,则AB2-4•OC2=________.
于A、B两点,将直线y=-x平移至经过点A,交x轴于C点,则AB2-4•OC2=________. 如图,直线y=kx交双曲线
如图,直线y=kx交双曲线 于A、B两点,将直线y=-x平移至经过点A,交x轴于C点,则AB2-4•OC2=______.
于A、B两点,将直线y=-x平移至经过点A,交x轴于C点,则AB2-4•OC2=______. 如图,直线y=kx交双曲线
如图,直线y=kx交双曲线 于A、B两点,将直线y=-x平移至经过点A,交x轴于C点,则AB2-4•OC2= .
于A、B两点,将直线y=-x平移至经过点A,交x轴于C点,则AB2-4•OC2= .