题目内容
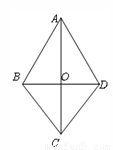
如图,在四边形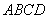 中,对角线
中,对角线 、
、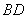 相交于点
相交于点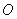 ,且
,且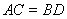 ,
,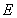 、
、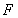 分别是
分别是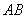 、
、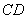 的中点,
的中点,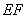 分别交
分别交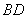 、
、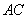 于点
于点 、
、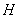 ,若
,若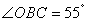 ,
, 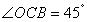 ,则
,则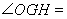 ???? .
???? .
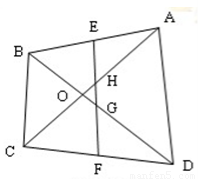
【答案】
50°.
【解析】
试题分析:取BC中点M,连接ME、FM,根据三角形中位线定理可得EM=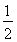 AC,MF=
AC,MF=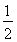 DB,EM∥AC,MF∥BD,然后再证明EM=MF,进而得到∠OHG=∠OGH,然后再结合三角形内角和定理可得答案.
DB,EM∥AC,MF∥BD,然后再证明EM=MF,进而得到∠OHG=∠OGH,然后再结合三角形内角和定理可得答案.
取BC中点M,连接ME、FM,
∵E、F分别是AB、CD的中点,
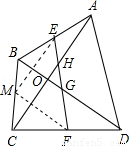
∴EM=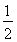 AC,MF=
AC,MF=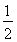 DB,EM∥AC,MF∥BD,
DB,EM∥AC,MF∥BD,
∵AC=BD,
∴EM=MF,
∴∠MEF=∠MFE,
∵EM∥AC,MF∥BD,
∴∠OHG=∠MEF,∠OGH=∠MFE,
∴∠OHG=∠OGH,
∵∠OBC=55°,∠OCB=45°,
∴∠BOC=180°﹣55°﹣45°=80°,
∴∠HOG=80°,
∴∠OGH=(180°﹣80°)÷2=50°,
故答案是50°.
考点:三角形中位线定理.

练习册系列答案
相关题目
 如图,在⊙M中,弧AB所对的圆心角为120°,已知⊙M的半径为2cm,并建立如图所示的直角坐标系.
如图,在⊙M中,弧AB所对的圆心角为120°,已知⊙M的半径为2cm,并建立如图所示的直角坐标系. 如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( )
如图,在?ABCD中,EF∥AB,MN∥BC,MN与EF交于点O,且O点在对角线上,图中面积相等的四边形有( ) 我们知道,小学对菱形的认识是:四条边都相等的四边形.到了初中,对菱形的定义是:有一组邻边相等的平行四边形,请你利用初中的定义来说明小学认识的合理性.先补全题目,再完成证明:
我们知道,小学对菱形的认识是:四条边都相等的四边形.到了初中,对菱形的定义是:有一组邻边相等的平行四边形,请你利用初中的定义来说明小学认识的合理性.先补全题目,再完成证明: 如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论:
如图,在四边形ABCD中(AB≠BC),AB∥CD,AB=CD,直线EF经过四边形ABCD的对角线AC和BD的交点O,且分别交AD、BC于点M、N,交BA、DC的延长线于点E、F,下列结论: 中,对角线AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有【
】
中,对角线AB=AD,CB=CD,若连接AC、BD相交于点O,则图中全等三角形共有【
】