题目内容
已知△ABC的高AD，BE所在的直线交于点O，∠C=42°，则∠AOB的度数为________．
138°或42°
分析：首先根据题意画出图形，注意此题分两种情况，一种是△ABC是锐角三角形，一种是△ABC是钝角三角形．
解答：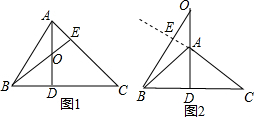
解：如图1所示：∵AD⊥BC，BE⊥AC，
∴∠ADC=∠CEB=90°，
∵∠EOD+∠OEC+∠ODC+∠C=360°，
∴∠EOD=360°-90°-90°-42°=138°；
如图2所示：
∵∴∠C=42°，
∴∠DAC=48°，
∴∠EAO=48°，
∴∠AOB=180°-90°-48°=42°，
故答案为：42°或138°．
点评：此题主要考查了三角形的高，关键是掌握四边形内角和为360°，注意要分类讨论．
分析：首先根据题意画出图形，注意此题分两种情况，一种是△ABC是锐角三角形，一种是△ABC是钝角三角形．
解答：
解：如图1所示：∵AD⊥BC，BE⊥AC，∴∠ADC=∠CEB=90°，
∵∠EOD+∠OEC+∠ODC+∠C=360°，
∴∠EOD=360°-90°-90°-42°=138°；
如图2所示：
∵∴∠C=42°，
∴∠DAC=48°，
∴∠EAO=48°，
∴∠AOB=180°-90°-48°=42°，
故答案为：42°或138°．
点评：此题主要考查了三角形的高，关键是掌握四边形内角和为360°，注意要分类讨论．
练习册系列答案
阅读快车系列答案
相关题目
如图所示，已知△ABC的高AD、BE交于H，△ABC、△ABH的外接圆分别为⊙O2和⊙O1，求证：⊙O与⊙O1的半径相等．
