题目内容
12.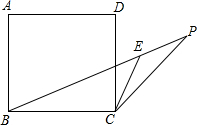 如图,在边长为2的正方形ABCD中CD边的右侧作CP=CD,连接BP,CE平分∠DCP交BP于E.求∠BEC的度数.
如图,在边长为2的正方形ABCD中CD边的右侧作CP=CD,连接BP,CE平分∠DCP交BP于E.求∠BEC的度数.
分析 由正方形的性质得出BC=CD,求出BC=CP,得出∠PBC=∠P,由三角形内角和定理得出2∠P+∠PCD=90°,由角平分线得出∠PCD=∠ECP,得出∠P+∠ECP=45°,即可得出∠BEC=45°.
解答 解:∵四边形ABCD是正方形,
∴BC=CD,
∵CP=CD,
∴BC=CP,
∴∠PBC=∠P,
∵∠PBC+∠P+∠BCP=180°,
∴2∠P+∠PCD+90°=180°,
∴2∠P+∠PCD=90°,
∵CE平分∠DCP,
∴∠PCD=∠ECP,
∴2∠P+2∠ECP=90°,
∴∠P+∠ECP=45°,
∵∠BEC=∠P+∠ECP,
∴∠BEC=45°.
点评 本题考查了正方形的性质、等腰三角形的性质、三角形内角和定理;熟练掌握正方形的性质,并能进行推理计算是解决问题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.按照国内生产总值(GDP)核算程序,国家统计局根据2011年有关统计年报和部门会计、财政决算资料,在初步核实的基础上,对2011年GDP数据进行了最终核实,2011年GDP现价总量约为4700000亿元,这一数据用科学记数法表示为( )
| A. | 4.7×106亿元 | B. | 0.47×106亿元 | C. | 4.7×104亿元 | D. | 47×104亿元 |
7.二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
下列结论中正确的有4个.
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)x=2是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<2时,ax2+(b-1)x+c>0.
| x | -1 | 0 | 0.5 | 2 |
| y | -1 | 2 | 3.75 | 2 |
(1)ac<0;
(2)当x>1时,y的值随x值的增大而减小;
(3)x=2是方程ax2+(b-1)x+c=0的一个根;
(4)当-1<x<2时,ax2+(b-1)x+c>0.
2.下列命题一定是真命题的是( )
| A. | 平分弦的直径必垂直于弦,且平分弦所对的两条弧 | |
| B. | 同一平面内,三点确定一个圆 | |
| C. | 三角形的外心到三角形三边的距离相等 | |
| D. | 圆的外切四边形的对边之和相等 |

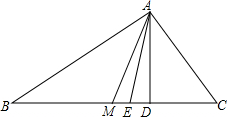 已知:如图,在△ABC中,AB>AC,AM是中线,AD是高,AE是角平分线,并且∠DAE=∠MAE,求证:∠BAC=90°.
已知:如图,在△ABC中,AB>AC,AM是中线,AD是高,AE是角平分线,并且∠DAE=∠MAE,求证:∠BAC=90°.