题目内容
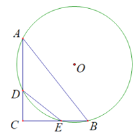
【题目】如图,在△ABC中,tan∠BAC![]() tan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
tan∠ABC=1,⊙O经过A、B两点,分别交AC、BC于D、E两点,若DE=10,AB=24,则⊙O的半径为( )
A.![]() B.
B.![]()
C.13D.![]()
【答案】C
【解析】
连接BO并延长,交圆O于点G,连接AG,AE,根据直径所对的圆周角是直角可得∠GAB=90°,从而证出∠G+∠GBA=90°,然后根据圆的内接四边形的性质可得∠AEC=∠G,根据锐角三角函数的性质可得△ABC为直角三角形,∠C=90°,然后根据圆周角定理证出![]() ,可得AG=DE=10,最后根据勾股定理求出直径即可求出结论.
,可得AG=DE=10,最后根据勾股定理求出直径即可求出结论.
解:连接BO并延长,交圆O于点G,连接AG,AE
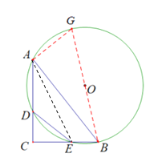
∴∠GAB=90°
∴∠G+∠GBA=90°
∵四边形AEBG是圆O的内接四边形
∴∠AEC=∠G
∴∠AEC+∠GBA=90°
∵tan∠BAC![]() tan∠ABC=1,
tan∠ABC=1,
∴△ABC为直角三角形,∠C=90°
∴∠AEC+∠EAC=90°
∴∠GBA =∠EAC
∴![]()
∴AG=DE=10
在Rt△AGB中
BG=![]()
∴⊙O的半径BO=![]() BG=13
BG=13
故选C.

练习册系列答案
相关题目