题目内容
 如图,大圆O的直径AB=24cm,分别以OA、OB为直径作⊙O1和⊙O2,并在圆⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4.这些圆互相内切或外切,则四边形O1O4O2O3的面积为________cm2.
如图,大圆O的直径AB=24cm,分别以OA、OB为直径作⊙O1和⊙O2,并在圆⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4.这些圆互相内切或外切,则四边形O1O4O2O3的面积为________cm2.
96
分析:连接O1O3,O2O3,O2O4,O1O4,O3O,根据相切两圆的性质得出O1O3=O2O3=O2O4=O1O4,得出菱形O1O4O2O3,推出O3O4⊥O1O2,O3O=O4O,求出O1O2=12,OO1=6,设⊙O3的半径是x,则O1O3=6+x,OO3=12-x,在Rt△OO1O3中,由勾股定理得出方程(6+x)2=62+(12-x)2,求出x,根据图形得出四边形O1O4O2O3的面积为2个△O1O3O2的面积,求出△O1O2O3的面积即可.
解答:
连接O1O3,O2O3,O2O4,O1O4,O3O,
∵根据相切两圆的性质得:O1O3=O2O3=O2O4=O1O4,
∴四边形O1O4O2O3是菱形,
∴O3O4⊥O1O2,O3O=O4O,
∵AB=24,
∴O1O2= AB=12,OO1=
AB=12,OO1= AB=6,
AB=6,
设⊙O3的半径是x,则O1O3=6+x,OO3=12-x,
在Rt△OO1O3中,由勾股定理得:(6+x)2=62+(12-x)2,
解得:x=4,
故四边形O1O4O2O3的面积为2个△O1O3O2的面积,是2× ×12×(12-4)=96,
×12×(12-4)=96,
故答案为:96.
点评:本题考查了菱形的性质和判定,三角形的面积.相切两圆的性质等知识的,题目综合性比较强,难度偏大,解此题的关键是得出四边形O1O3O2O4是菱形和求出⊙O3的半径.
分析:连接O1O3,O2O3,O2O4,O1O4,O3O,根据相切两圆的性质得出O1O3=O2O3=O2O4=O1O4,得出菱形O1O4O2O3,推出O3O4⊥O1O2,O3O=O4O,求出O1O2=12,OO1=6,设⊙O3的半径是x,则O1O3=6+x,OO3=12-x,在Rt△OO1O3中,由勾股定理得出方程(6+x)2=62+(12-x)2,求出x,根据图形得出四边形O1O4O2O3的面积为2个△O1O3O2的面积,求出△O1O2O3的面积即可.
解答:

连接O1O3,O2O3,O2O4,O1O4,O3O,
∵根据相切两圆的性质得:O1O3=O2O3=O2O4=O1O4,
∴四边形O1O4O2O3是菱形,
∴O3O4⊥O1O2,O3O=O4O,
∵AB=24,
∴O1O2=
 AB=12,OO1=
AB=12,OO1= AB=6,
AB=6,设⊙O3的半径是x,则O1O3=6+x,OO3=12-x,
在Rt△OO1O3中,由勾股定理得:(6+x)2=62+(12-x)2,
解得:x=4,
故四边形O1O4O2O3的面积为2个△O1O3O2的面积,是2×
 ×12×(12-4)=96,
×12×(12-4)=96,故答案为:96.
点评:本题考查了菱形的性质和判定,三角形的面积.相切两圆的性质等知识的,题目综合性比较强,难度偏大,解此题的关键是得出四边形O1O3O2O4是菱形和求出⊙O3的半径.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图,大圆O的直径AB=acm,分别以OA、OB为直径作⊙O1、⊙O2,并在⊙O与⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4,这些圆互相内切或外切,则四边形O1O2O3O4的面积为
如图,大圆O的直径AB=acm,分别以OA、OB为直径作⊙O1、⊙O2,并在⊙O与⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4,这些圆互相内切或外切,则四边形O1O2O3O4的面积为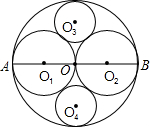 (2012•中江县二模)如图,大圆O的直径AB=24cm,分别以OA、OB为直径作⊙O1和⊙O2,并在圆⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4.这些圆互相内切或外切,则四边形O1O4O2O3的面积为
(2012•中江县二模)如图,大圆O的直径AB=24cm,分别以OA、OB为直径作⊙O1和⊙O2,并在圆⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4.这些圆互相内切或外切,则四边形O1O4O2O3的面积为

