题目内容
 如图,大圆O的直径AB=acm,分别以OA、OB为直径作⊙O1、⊙O2,并在⊙O与⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4,这些圆互相内切或外切,则四边形O1O2O3O4的面积为
如图,大圆O的直径AB=acm,分别以OA、OB为直径作⊙O1、⊙O2,并在⊙O与⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4,这些圆互相内切或外切,则四边形O1O2O3O4的面积为分析:根据半径的关系可得出O1O2O3O4为菱形,然后设出小圆半径,在RT△O1OO3中解出小圆半径,从而根据菱形的面积=2SO1O2O3从而可求出面积.
解答: 解:由题意知:O1O4=O4O2=O2O3=O3O1,
解:由题意知:O1O4=O4O2=O2O3=O3O1,
∴四边形O1O3O2O4是菱形,
∴O1O2⊥O3O4,
∵大圆O的直径AB=acm,
∴O1O2=
,
设小圆半径为x,则在Rt△O1OO3中,
(
a)2+(
a-x)2=(
a+x)2,
解得:x=
a,
∴菱形的面积=2SO1O2O3=
×
a×(a-
a)]=
a2.
故答案为:
a2.
 解:由题意知:O1O4=O4O2=O2O3=O3O1,
解:由题意知:O1O4=O4O2=O2O3=O3O1,∴四边形O1O3O2O4是菱形,
∴O1O2⊥O3O4,
∵大圆O的直径AB=acm,
∴O1O2=
| a |
| 2 |
设小圆半径为x,则在Rt△O1OO3中,
(
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 4 |
解得:x=
| 1 |
| 6 |
∴菱形的面积=2SO1O2O3=
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 6 |
| 1 |
| 6 |
故答案为:
| 1 |
| 6 |
点评:本题考查了相切圆的性质,难度较大,关键是求出小圆的半径及判断出O1O2O3O4的形状.

练习册系列答案
相关题目
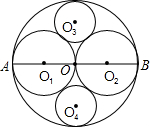 (2012•中江县二模)如图,大圆O的直径AB=24cm,分别以OA、OB为直径作⊙O1和⊙O2,并在圆⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4.这些圆互相内切或外切,则四边形O1O4O2O3的面积为
(2012•中江县二模)如图,大圆O的直径AB=24cm,分别以OA、OB为直径作⊙O1和⊙O2,并在圆⊙O1和⊙O2的空隙间作两个等圆⊙O3和⊙O4.这些圆互相内切或外切,则四边形O1O4O2O3的面积为

