题目内容
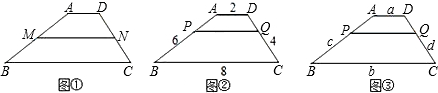
如图,一条两边平行的纸带的宽度(两平行线间的距离)为8cm,现将纸带折起压平(两条相对的长边应相交),那么重叠部分△ABC面积的最小值为

- A.16cm2
- B.32cm2
- C.64cm2
- D.无最小值
B
分析:由于两直线平行,且平行线间的距离为8cm,故△ABC的高不变,当三角形的底边AC最短时,三角形的面积最小.
解答:当AC⊥AB时,
由折叠的性质可知,AC=AB=8cm,
此时三角形的面积最小,
S最小值= ×8×8=32cm2.
×8×8=32cm2.
故选B.

点评:此题考查了翻折变换,根据翻折不变性和矩形的性质及三角形的面积公式,判断出当底边最短时三角形的面积最小是解题的关键.
分析:由于两直线平行,且平行线间的距离为8cm,故△ABC的高不变,当三角形的底边AC最短时,三角形的面积最小.
解答:当AC⊥AB时,
由折叠的性质可知,AC=AB=8cm,
此时三角形的面积最小,
S最小值=
 ×8×8=32cm2.
×8×8=32cm2.故选B.

点评:此题考查了翻折变换,根据翻折不变性和矩形的性质及三角形的面积公式,判断出当底边最短时三角形的面积最小是解题的关键.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目